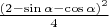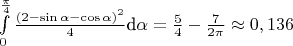Есть 8 шаров, среди которых 6 заряжены нейтрально, один - положительно и один - отрицательно. Есть прибор, который, будучи поднесённым к группе шаров, покажет их общий заряд (он покажет 0 и если в группе нет ни одного заряженного шара, и если они там оба).
За какое наименьшее число измерений можно найти положительный и отрицательный шары в группе?
================
Решение
Сначала оценим снизу необходимое число измерений. Поскольку вариантов выбора положительного и отрицательного шара из 8 будет
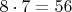 , а одно измерение может сократить количество вариантов не более чем втрое, то менее чем за
, а одно измерение может сократить количество вариантов не более чем втрое, то менее чем за 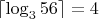 измерения задачу решить нельзя.
измерения задачу решить нельзя.Первое измерение нужно спланировать так, чтобы при каждом его исходе оставалось не более 27 вариантов.
Если выбрать для него 1 или 2 шара, прибор покажет 0 в 42 или в 32 случаях. При выборе трёх шаров для первого измерения (скажем, шары 1, 2 и 3), нейтральный заряд будет зафиксирован в 26 случаях, ещё по 15 вариантов распределения зарядов среди шаров дадут положительное и отрицательное показания. Эти случаи удобно рассмотреть в виде таблицы. Кадая её ячейка – это показание прибора в случае возможной пары шаров, заряженных положительно (по вертикали) и отрицательно (по горизонтали).

Вторым измерением 26 вариантов, давших нейтральное показание, нужно разбивать на 9+9+8.
Покажем, что это невозможно. Включения шаров из групп 1-3 и 4-8 независимо влияет на количества возможных показаний прибора. Если из шаров 1-3 выбрать в измеряемую группу 0 или 3 шара, то среди исходов измерения 6 раз встретится 0, и ни разу – плюс или минус. Для краткости запишем это так: 0 (-), 0 (+), 6 (0). Если же выбрать 1 или 2 шара, то среди исходов будут 2(-), 2(+), 2 (0)
Если из шаров 4-8 для измерения брать 0 или 5 шаров, то среди сиходов будут 0 (-), 0 (+), 20 (0). Если брать 1 или 4 шара, то 4 (-), 4 (+), 12 (0). И 2 или 3 шара, включённые в измеряемую группу, покажут 6(+), 6(-), 8(0).
Таким образом, наилучшее, чего можно добиться вторым измерением – это разбитие 26 вариантов на 8+8+10, выбрав, к примеру, 1, 7 и 8 шары

Значит, измерение первым действием трёх шаров к цели за 4 шага не приведёт. Попробуем измерить сначала 4 шара. Получаем следующее распределение исходов:

Довольно перспективный расклад: 16(+), 16(1), 24(0). Более того, в случае нейтрального результата в измерении 1, вторым замером эти 24 варианта разбиваются на 8+8+8 (и только так, расклады 9+9+6 и 9+8+7 невозможны), взяв шары №№3, 4, 5, 6.

И в случае нейтрального результата второго измерения на подозрении остаются 8 упорядоченных пар (положительный шар; отрицательный шар): (1;2), (2;1), (3;4), (4;3), (5;6), (6;5), (7;8), (8;7), Их можно разделить на 3+3+2, замерив шары 1, 3, 5. В таком случае прибор покажет:
«+» при (1;2), (3;4) или (5;6) – здесь для 4го измерения выберем пару №№1,4,
«–» - при (2;1), (4;3) или(6;5) – и здесь тоже,
и «0» при (7;8) или (8;7) – а тут достаточно узнать знак шара №8.
Итак, оставшимся четвёртым измерением можно однозначно найти искомые заряды.
Но в случае положительного результата второго измерения на подозрении будут такие 8 пар:
(3;1), (3;2), (4;1), (4;2), (5;7), (5;8), (6;7), (6;8). Применив соображения, аналогичные доказательству невозможности разбить 26 вариантов на 9+9+8, приходим к выводу, что невозможно выбрать такую группу шаров, чтобы третьим измерением разбить эти 8 вариантов на 3+3+2.
Таким образом, 4 измерения может и не хватить. Построим метод, дающий гарантированный результат за 5 замеров. В текущей ветке 8 вариантов легко разделить трёхкратной дихотомией.
В случае же, если после первого замера будет ненулевй исход (скажем, «+»), положительный шар находится среди 4 шаров, а отрицательный – среди остальных 4 шаров. На нахождение каждого дихотомией потребуется по 2 замера – итого в 5 укладываемся.
Обсуждение
Собственно задачу я сформулировал как модификацию известной задачи о поиске радиоактивных шаров. Введение зарядов, с одной стороны, удваивает возможные расположения шаров для заданного n, а с другой – предоставляет возможность каждым измерением делить это количество не на 2, а на 3.
Однако из-за того, что не непосредственно разделяем созможные варианты ответа на группы, а посредством выбора некоторой группы шаров, точное деление на 3 оказывается возможным далеко не всегда. И основной сложностью в этой задаче является именно доказательство невозможности уложиться в 4 измерения. При этом ветка, показывающая невозможность начинается после нулевого результата первого измерения и ненулевого - второго, а не после обоих нулевых результатов, как писали некоторые участники марафона.
Интересным был подход рассмотреть задачу как систему линейных уравнений с 8 неизвестными, в которую каждое новое измерение добавляет уравнение. Однако автор решения не учёл, что сами переменные могут принимать только 3 допустимых значения.
Напрашивается обобщение задачи: за сколько измерений можно найти положительный и отрицательный шар для произвольного общего количества шаров n?
Оценкой снизу для искомой функции
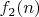 будет
будет  , сверху в первом приближении можно взять n-1 – достаточно проверить все шары, кроме одного.
, сверху в первом приближении можно взять n-1 – достаточно проверить все шары, кроме одного.Для небольших n можно построить таблицу:
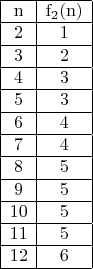
Сергей Половинкин, помимо таблицы, строит алгоритм нахождения заряженных шаров для произвольного n и показывает, что
![$f_2(n)=[ \log_2 n ] + [ \log_2 \frac n3 ] + 1$ $f_2(n)=[ \log_2 n ] + [ \log_2 \frac n3 ] + 1$](http://dxdy.ru/math/b52cfa7445942c4b0ea0be122c1777c182.gif) .
.Я предлагаю создать отдельную тему для обсуждения алгоритмов решения этой и аналогичных задач, опубликовав полный алгоритм там
Награды
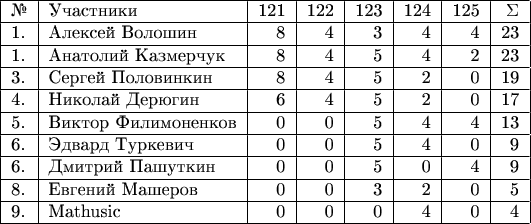
Виктор Филимоненков и Алексей Волошин за правильное решение задачи получают по 4 балла. Сергей Половинкин, проведя очень интересное обобщение, в доказательстве невозможности решить текущую задачу за 4 измерения, привёл пример ветки, которая на самом деле за 4 измерения решается. Таким образом, он получает 3+2 (бонус за развитие темы)=5 баллов. Анатолий Казмерчук получает 3 балла, Эдвард Туркевич получает 2 балла, Николай Дерюгин и Евгений Гужавин получают по 1 баллу.
Эстетическая оценка задачи 4.4
================
Разбор задачи ММ126 подготовлен Алексеем Изваловым.
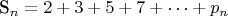 - сумма n первых простых чисел.
- сумма n первых простых чисел. 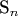 является простым тогда и только тогда, когда существует такое простое число q, что
является простым тогда и только тогда, когда существует такое простое число q, что 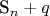 кратно
кратно 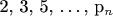 .
.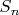 существует. Тогда
существует. Тогда 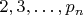 . Действительно, если
. Действительно, если 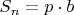 , где p - одно из первых n простых, и
, где p - одно из первых n простых, и 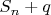 кратно p, то и q кратно p, а поскольку q простое, то q = p. Тогда
кратно p, то и q кратно p, а поскольку q простое, то q = p. Тогда  - делится на
- делится на  , в то время как
, в то время как 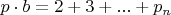 . То есть сумма n чисел, не меньших 2, лишь на одно слагаемое меньше их произведения, что для суммы первых протсых чисел, очевидно, не верно начиная с
. То есть сумма n чисел, не меньших 2, лишь на одно слагаемое меньше их произведения, что для суммы первых протсых чисел, очевидно, не верно начиная с 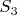 (для
(для 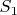 и
и 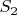 утверждение доказывается непосредственно).
утверждение доказывается непосредственно).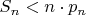 , а поскольку
, а поскольку 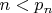 , то
, то 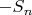 и разностью
и разностью  . Поскольку
. Поскольку 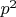 , не может иметь делителей, больших p", я был близок к "кровопролитию". Но сдержался :)
, не может иметь делителей, больших p", я был близок к "кровопролитию". Но сдержался :) 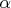
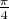 .
.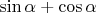 (такую картинку можно видеть в индийском доказательстве теоремы Пифагора). Центр этого квадрата совпадает с центром монеты. Пересечение описанного вокруг монеты квадрата с ячейкой равносильно пересечению самой монеты с ячейкой.
(такую картинку можно видеть в индийском доказательстве теоремы Пифагора). Центр этого квадрата совпадает с центром монеты. Пересечение описанного вокруг монеты квадрата с ячейкой равносильно пересечению самой монеты с ячейкой.
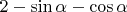 . Тогда вероятность того, что при данном угле
. Тогда вероятность того, что при данном угле