Оценка за решение задачи ММ125 учитывается дважды в основном Марафоне и в тематическом конкурсе.
ММ125 (КГ-8) (4 балла)
Верно ли, что группа автоморфизмов структурного графа любого n-угольника изоморфна подгруппе группы диэдра n-й степени?
================
Решение
Приведу решение Алексея Волошина.
Рассмотрим правильный (можно любой выпуклый, но так удобнее) пятиугольник ABCDE. Точку пересечения диагоналей BD и CE обозначим через A', точку пересечения AD и CE - через B', и т. д.
У структурного графа пятиугольника ABCDE есть пять автоморфизмов, соответствующих поворотам и пять автоморфизмов, соответствующих отражениям пятиугольника. Каждый из них внешние вершины переводит во внешние, а внутренние - во внутренние. Но кроме этого, существует "выворачивающий" автоморфизм, который меняет местами вершины A и A', B и B', C и С', D и D', E и E'. В композиции с поворотами и отражениями это даёт ещё десять автоморфизмов. Итого - 20 автоморфизмов, в то время как группа диэдра 5-й степени содержит всего 10 элементов.
Обсуждение
Группа автоморфизмов структурного графа пятиугольника является единственным исключением. Для остальных многоугольников ответ на вопрос задачи положителен. Это следует из того, что при n, отличном от 5, любой автоморфизм структурного графа выпуклого n-угольника задает автоморфизмом циклического подграфа, образованного вершинами, соответствующими вершинам исходного многоугольника, и, в свою очередь, однозначно определен автоморфизмом этого подграфа. Рассуждение такого рода содержится в решении Анатолия Казмерчука. Однако Анатолий исходил из неверного тезиса об обязательном изоморфизме групп автоморфизмов структурного и сопровождающего графов и поэтому прозевал случай n = 5.
Отмечу, что, кроме упомянутого случая n = 5, группы автоморфизмов структурного и сопровождающего графов выпуклого n-угольника не изоморфны еще и при n = 3.
Задача ММ125 оказалась в некотором смысле парадоксальной. Я считал ее весьма легкой (это отражено и в цене задачи). Мое мнение, с одной стороны, подтверждается мнениями ряда участников Марафона, отметивших простоту ММ125, а с другой стороны, опровергается количеством марафонцев, осиливших эту задачу.
Награды
За правильное решение этой задачи Виктор Филимоненков, Алексей Волошин и Дмитрий Пашуткин получают по 4 призовых балла. Анатолий Казмерчук получает 2 призовых балла.
Эстетическая оценка задачи 4.4
================
Обзор задачи ММ125 подготовлен Владимиром Лецко
================
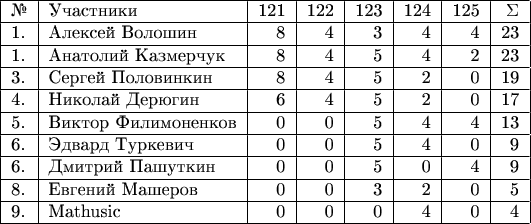
Текущее положение участников
в XIII туре Математического марафона
Комментариев нет:
Отправить комментарий