Разбор задачи ММ122 математического марафона

===============

Задача ММ122 является прямым продолжением задачи ММ57.
Оценка за решение задачи ММ122 учитывается дважды в основном Марафоне и в тематическом конкурсе.

ММ122 (КГ-7) (4 балла)

1. Найти формулу для выражения числа вершин структурного графа с данным характеристическим вектором.
2. Найти формулу для выражения числа элементарных многоугольников исходного многоугольника с данным характеристическим вектором.


================

Решение

Будем использовать обозначения принятые в преамбуле к тематическому конкурсу 13-го тура Марафона.

Число вершин структурного графа ординарного многоугольника зависит только от n и, являясь суммой числа точек пересечения диагоналей и числа вершин исходного многоугольника, подсчитывается по формуле

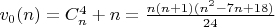
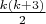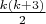Легко доказать индукцией по k, что каждая особенность порядка k уменьшает количество вершин структурного графа на . Поэтому число вершин структурного графа многоугольника с характеристическим вектором s вычисляется по формуле: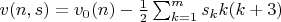

Формула для подсчета числа вершин сопровождающего графа ординарного n-угольника получается применением соотношения Эйлера (подробности см.в ММ57) для плоской укладки планарного графа:

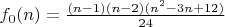
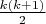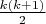Наличие полюса k-того порядка уменьшает количество вершин сопровождающего графа на . Поэтому для n-угольника с характеристическим вектором S имеем следующую формулу для числа вершин сопровождающего графа: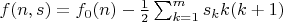

Обсуждение

Легко вывести и формулу для подсчета числа ребер структурного (дуального) графа:

,

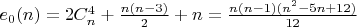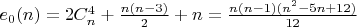где - число ребер структурного графа ординарного n-угольника.

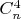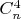Доказательство того, что в ординарном четырехугольнике ровно точки пересечения диагоналей, совершенно очевидно. В самом деле, каждая четверка вершин определяет ровно одну точку пересечения диагоналей. И обратно.

Однако мои многолетние наблюдения показывают, что эта очевидность совершенно не очевидна :)

Вместо приведенного выше наблюдения многие начинают подсчитывать число точек пересечения диагоналей значительно более хитрыми методами. Например, суммируя интересующие нас точки по каждой диагонали.

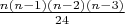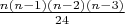Так поступают практически все хорошие студенты (плохие не поступают никак), которым я предлагал найти формулу для числа точек пересечения диагоналей ординарного n-угольника. Схожим путем пошли и несколько участников Марафона. Признаюсь, что в свое время и я, впервые столкнувшись с этой задачкой, шел к ответу окольным путем. И только преобразовав итоговую формулу к виду , увидел короткий путь.

Награды

За правильное решение этой задачи Сергей Половинкин, Алексей Волошин, Анатолий Казмерчук и Николай Дерюгин получают по 4 призовых баллов.

Эстетическая оценка задачи - 4.3 балла

================

Обзор задачи ММ122 подготовлен Владимиром Лецко