Разбор задачи ММ141 Математического Марафона

======= 141 ========

ММ141 (3 балла)

Существуют ли натуральные числа 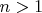такие, что 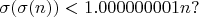( 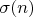- сумма натуральных делителей числа .)

===============

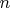Решение

Проще всего найти подходящее число, взяв достаточно большое (больше 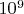) простое число 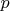так, чтобы 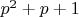тоже было простым. Тогда в качестве 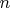подойдет .
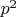Наименьшее подходящее 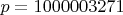. Тогда 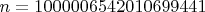, 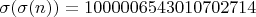и .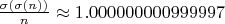

Обсуждение

Не обязательно добиваться простоты числа 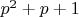. Достаточно, чтобы оно не имело малых простых делителей.
Например, iPhonograph взял 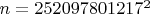. Тогда 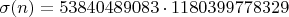и .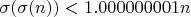
Эта идея - использовать отсутствие малых множетелей вместо простоты - позволила Андрею Халявину доказать то, что, по сути, было очевидно и остальным участникам. А именно: для любого 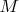найдутся натуральные 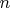такие, что .
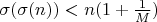В самом деле, большинству участников (и ведущему) представляется очевидным, что существует бесконечно много простых 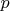таких, что 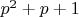тоже просто. Но "представляется очевидным" - не доказательство.
Андрей же доказал, что для каждого достаточно большого простого числа 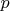найдется показатель степени 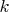(ну очень большой!) такой, что 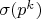не имеет малых делителей. И отсюда получить требуемое утвержденеие.

Гораздо более интересной, чем ММ141 является такая задача: Существуют ли натуральные числа 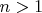такие, что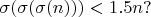
Но эту задачу мне решить не удалось. Ясно, что необходимым (но недостаточным) условием является существование такого натурального 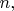что числа 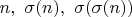- нечетны.
Единственный извесстный мне нетривиальный пример дает число .

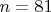Награды

За правильное решение задачи ММ141 Алексей Волошин, Сергей Половинкин, Николай Дерюгин, Евгений Гужавин, iPhonograph, Sirion и Анатолий Казмерчук получают по 3 призовых балла. За правильное решение более общей задачи Андрей Халявин получает 5 призовых баллов. За верные идеи (не доведенные до конца) Александр Ларин и Кирилл Веденский получают 2 и 1 балл, соответсвенно.

Эстетическая оценнка задачи 4 балла

Разбор задачи ММ141 подготовил Владимир Лецко