Разбор задачи ММ150 Математического Марафона

======= 150 ========

ММ150 (12 баллов)

Каждому n-угольнику поставим в соответствие ожерелье из n бусин белого, зеленого и красного цветов следующим образом: свободой стороне соответствует белая бусина; полусвободной - зеленая; зажатой - красная.
Два n-угольника назовем эквивалентными, если им соответствуют одинаковые ожерелья (ожерелье не меняется при поворотах и переворачивании). На сколько классов эквивалентности разобьются 20-угольники?

====================

Решение

Еще раз приведу решение Андрея Халявина.

Расставим черные бусины в углы многоугольника, которые меньше развернутого, и белые - в углы больше развернутого.
Конфигурация черных и белых бусин однозначно определяет цвет сторон. В обратную сторону однозначность нарушается, только если все стороны зеленые. Но возникающие при этом две две конфигурации переводятся друг в друга поворотом.
Таким образом задача свелась к подсчету числа ожерелий из бусин двух цветов. При этом черных бусин не меньше трех, так как в многоугольнике не меньше трех углов, меньших развернутого. (Для доказательства достаточно рассмотреть выпуклую оболочку исходного многоугольника.)
С другой стороны, любая конфигурация, в которой не менее трех черных бусин, очевидно, возможна. (Достаточно взять правильный 20-угольник и вдавить внутрь вершины, соответствующие белым бусинам.)

Подсчитаем количество черно-белых ожерелий без учета ограничения, что черных бусин не менее трех.
Воспользуемся леммой Бернсайда. В качестве группы преобразований 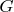выступает группа диэдра, состоящая из 20-и симметрий и 20-и поворотов (включая тождественный).
Если 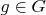- симметрия, ось которой проходит через две бусины, то для 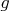имеется 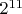неподвижных конфигураций. Если же ось симметрии не проходит через бусины, для 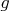имеется 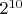неподвижных конфигураций. Значит, вклад симметрий .
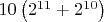Для поворотов имеем сумму 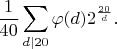Итого получаем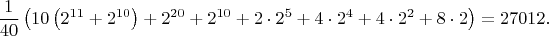

Очевидно, что существует ровно одно ожерелье из белых бусин, одно ожерелье с одной черной бусиной и 10 ожерелий с двумя черными бусинами. Поэтому окончательно получаем 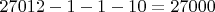классов 20-угольников.


Обсуждение

Задача о подсчете числа ожерелий широко известна. Наиболее подробное и доступное изложение (среди известных мне) можно найти в книге Дж. Андерсона "Дискретная математика и комбинаторика".

Разумеется, вместо 20-угольников можно было рассматривать произвольные n-угольники. Число 20 привлекло меня красотой ответа, являющегося в этом случае круглым числом и, к тому же, полным кубом!

С помощью леммы Бернсайнда можно вывести и явную формулу для подсчета ожерелий, в которых число бусин каждого цвета фиксировано. Например, число черно-белых ожерелий из 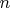бусин, среди которых и 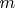черных, подсчитывается по формуле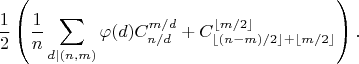
Вывод этой формулы можно посмотреть, например, здесь.
При 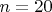, суммируя по всем , вновь получим 27000.

Интересно, что если не различать полусвободные и зажатые стороны, задача станет сложнее.
Пусть свободным сторонам соответствуют белые бусины, а прочим - красные. Если сторона не является свободной, то хотя бы одна из соседних с ней сторон тоже не является свободной. Поэтому красная бусина не может быть окружена белыми. Таким образом, при 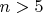интересующее нас число классов равно количеству ожерелий, которые можно составить из n белых и красных бусин, при условии, что никакая красная бусина не окружена белыми.
Я посчитал количество классов для всех (например, при 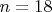получается 799 классов), но общей формулы мне вывести не удалось.

В заключение еще об одной классификации, для которой мне не удалось вывести общую формулу для подсчета числа классов.
Будем считать эквивалентными n-угольники, у которых поровну как внутренних, так и внешних диагоналей.
Можно показать, что число классов не превосходит 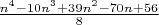. Но, начиная с 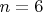, эта оценка завышена.


Награды

За правильное решение задачи ММ150 Алексей Волошин, Анатолий Казмерчук и Андрей Халявин получают по 12 призовых баллов. Сергей Половинкин получает 11, Виктор Филимоненков - 9 призовых баллов.

Эстетическая оценка - 4.7 балла

Разбор задачи ММ150 подготовил Владимир Лецко

-- 01 ноя 2011, 19:36 --

Итоговое положение участников в тематическом конкурсе
XV тура Математического марафона



=================================

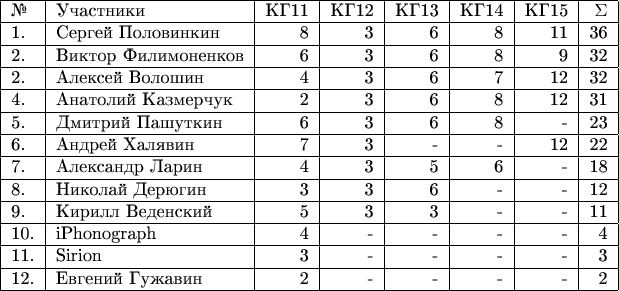
Итоговое положение участников в XV туре Математического марафона



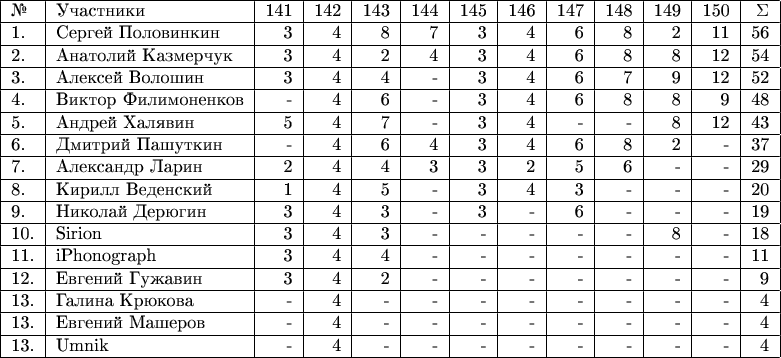
Мои поздравления лауреатам!