ММ147 (КГ13) (6 баллов)
Какое наименьшее число внутренних диагоналей может иметь n-угольник, у которого ровно один угол больше развернутого?
====================
Решение
Воспользуюсь чертежом Анатолия Казмерчука:

Размеcтив вершину
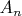 внутри треугольника, образованного стороной
внутри треугольника, образованного стороной 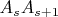 и диагоналями
и диагоналями 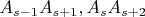 , добьемся максимального для данного
, добьемся максимального для данного  числа диагоналей, не являющихся внутренними.
числа диагоналей, не являющихся внутренними.Ясно, что внутренними будут диагонали
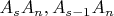 , а также диагонали выпуклых многоугольников,
, а также диагонали выпуклых многоугольников,  и
и 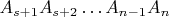 .
. Число диагоналей, не являющихся внутренними, будет наибольшим, когда количества вершин от
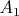 до
до 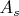 и от
и от 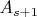 до
до 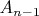 будут равны или максимально близки между собой (произведение целых положительных сомножителей с постоянной суммой максимально, когда сомножители максимально близки между собой).
будут равны или максимально близки между собой (произведение целых положительных сомножителей с постоянной суммой максимально, когда сомножители максимально близки между собой).При нечетных
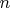 и
и 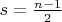 получим
получим 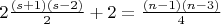 .
. При четных
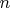 и
и 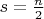 наименьшее число внутренних диагоналей будет
наименьшее число внутренних диагоналей будет 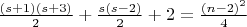 .
.Обсуждение
Тот же ответ можно получить, вычитая из общего число диагоналей исходного многоугольника число диагоналей, не являющихся внутренними.
Например, для нечетного
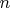 имеем:
имеем: 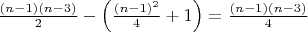 .
.Замечу, что среди диагоналей, не являющихся внутренними, одна (на рисунке это
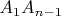 обязательно является внешней. Но внешних диагоналей может быть и более одной. Впрочем, на ход решения и ответ это обстоятельство никак не влияет.
обязательно является внешней. Но внешних диагоналей может быть и более одной. Впрочем, на ход решения и ответ это обстоятельство никак не влияет. Оба ответа можно объединить в один. Например, так:
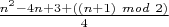 .
.Награды
За правильное решение задачи ММ147 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Николай Дерюгин и Дмитрий Пашуткин получают по 6 призовых баллов. Александр Ларин получает 5, а Кирилл Веденский - 3 призовых балла.
Эстетическая оценка - 4.4 балла
Разбор задачи ММ147 подготовил Владимир Лецко
Комментариев нет:
Отправить комментарий