23 ноября 2011

Разбор задачи ММ146 Математического Марафона

======= 146 ========

ММ146 (4 балла)

При каких 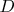$D$ существуют графы диаметра 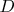$D$, у которых сумма квадратов степеней вершин равна $D^2$?

====================

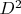Решение

Сумма степеней вершин, а следовательно и сумма квадратов степеней вершин, любого графа - четна. Поэтому для нечетных D решений нет.
При 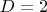$D=2$ наименьшее значение суммы квадратов степеней вершин достигается у двухзвенной цепочки и равно 6. Поэтому 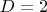$D=2$ тоже не годится.
Не подходит и 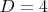$D=4$. У цепи длины 4 сумма квадратов степеней вершин - 14. Но добавление любой вершины (любых вершин) без изменения диаметра увеличивает минимум на $1+(3^2-2^2)=6$.
Покажем, что для всех четных $D \ge 6$ нужные графы имеются.
Возьмем цепь длины 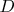$D$ и будем добавлять к вершинам отличным от концевых висячие вершины: к одной - 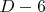$D-6$; к одной - 2; к 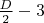$\frac D2-3$ - по одной.
Сумма степеней вершин полученного графа составит $(D-4)^2+4^2+\left(\frac D2-3\right)\cdot{3^2}+\frac D2 \cdot 2^2+(2+(D-6)+2+\frac{D}2-3)\cdot 1=D^2$.

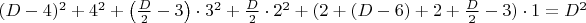Обсуждение

Существует много различных способов построения подходящих графов для четных $D \ge 6$. Вариант приведенный в решении предложен Кириллом Веденским и Анатолием Казмерчуком.
Еще один универсальный метод предложен Виктором Филимоненковым: к одной из внутренних вершин вершин цепи длины 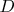$D$ прицепим 2 висячие вершины, а к другой - 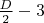$\frac D2-3$ трехвзенных цикла.
Другие подходы (в том числе и авторский) либо содержат исключения для малых значений 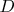$D$, либо варьируются, например, в зависимости от $D \ mod \ 4$.

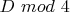Уже не в первый раз (хотя я и не смог найти в архиве, когда был первый раз) некоторые марафонцы загадочным образом ухитряются найти диаметр графа, не являющегося связным. Насколько я в курсе (а я, полагаю, в курсе), диаметр (как и расстояние, через которое он вводится) определяется только для связного графа.

Награды

За правильное решение задачи ММ146 Анатолий Казмерчук, Виктор Филимоненков, Алексей Волошин, Сергей Половинкин, Дмитрий Пашуткин, Кирилл Веденский и Андрей Халявин получают по 4 призовых балла. Александр Ларин получает 2 призовых балла.

Эстетическая оценка - 4.6 балла

Разбор задачи ММ146 подготовил Владимир Лецко
Labels: ,

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)