17 октября 2010

Разбор задачи ММ129 математического марафона

================

ММ129

Будем заполнять бесконечный клетчатый лист бумаги натуральными числами по спирали (каждый следующий виток начинается на вертикали, в которой стоит единица):

Изображение

Для каждого числа найдём восемь модулей разности его с соседями (по вертикали, горизонтали и диагонали). Количество простых чисел среди этих восьми назовем индексом простоты окружения исходного сила.
Какое наибольшее значение может принимать индекс простоты окружения?
Для скольких чисел достигается это значение?

================

Решение.

Для числа 2 имеем индекс простоты, равный 5. Докажем, что больше чисел с таким индексом быть не может. Для соседей единицы их индексы простоты проверяются непосредственно, а для остальных чисел справедливы следующие рассуждения.

Поскольку от витка к витку количество цифр увеличивается на 4, то т.к. четные/нечётные числа стоят столбцами. Значит, у каждого числа среди восьми разностей шесть будут нечётными.

Поскольку при данном способе заполнения в соседних клетках не будут стоять чисел, различающихся на 2, то и простых разностей не будет больше 6.
Но по правилу построения для большинства чисел две из нечётных разностей будут единицами. Ровно одна разность будет равняться одному для чисел в двух столбцах: идущем вверх от единицы и смежном с ним слева.

Рассмотрим число, стоящее в столбце, идущем вверх от единицы.
Общий вид такого числа 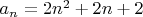$a_n=2n^2+2n+2$ (если начинать индекс n с нуля).
Соседями его будут:
$(a_{n+3}-1),~(a_{n+1}),~(a_{n+2}+1)$
$(a_{n+2}-1),~(a_{n}),~(a_{n+1}+1)$
$(a_{n+1}-1),~(a_{n-1}),~(a_{n}+1)$

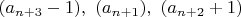
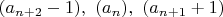
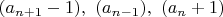
Разностями - кандидатами в простые будут:
Северо-запад: $12n+23$
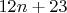
Запад: $8n+11$
Юго-запад: $4n+3$
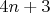
Северо-восток: $8n+13$
Восток: $4n+5$

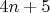
Но, перебирая возможные остатки от деления n на 3, увидим, что среди этих чисел хотя бы одно будет делиться на 3. Т.к. ровно трём разность не может равняться, то среди разностей будет не более четырёх простых.

Теперь рассматриваем смежный слева столбец. Числа этого столбца, смежные с 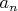$a_{n}$, будут иметь вид 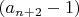$(a_{n+2}-1)$ Соседями их будут: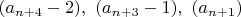
$(a_{n+4}-2),~(a_{n+3}-1),~(a_{n+1})$
$(a_{n+3}-2),~(a_{n+2}-1),~(a_{n})$
$(a_{n+2}-2),~(a_{n+1}-1),~(a_{n-1})$

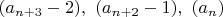
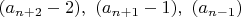
Северо-запад: $8n+27$
Запад: $4n+11$
Северо-восток: $4n+7$
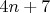
Восток: $8n+11$
Юго-восток: $12n+11$

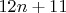
И, опять-таки, не больше четырёх из этих разностей будут простыми.

Обсуждение

Задачу про спиральное заполнение гексагональной сетки я решал, участвуя в турнире Эйлера на сайте Диофант.ру. Мне понравилось, что за несколько пугающим построением, заставляющем прикинуть возможность моделирования всего процесса на компьютере, кроется эффектный шаг, устраняющий эту необходимость.

Награды

За правильное решение задачи Виктор Филимоненков, Алексей Волошин, Анатолий Казмерчук, Сергей Половинкин и Пашуткин Дмитрий получают по 5 баллов.

Эстетическая оценка задачи 5

================

Разбор задачи ММ129 подготовил Алексей Извалов
Labels: , , ,

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)