
Чтобы занять область, нужно решить 1 задачу:
Задача 10
Сфера поделена на государства, и границами служат 17 больших кругов этой сферы. Ни в одной точке не граничат более 4 государств. Путешественник утверждает, что объехал все государства наземным транспортом, побывав в каждом по одному разу и не проезжая точки, где граничат какие - либо 4 государства. Могло ли так быть?
К карте математического острова
Решенные задачи:
Задача 1. Два лыжника двигались со скоростью 12 км/ч. При входе на сложный участок их скорость уменьшилась до 8 км/ч. Когда оба лыжника оказались на сложном участке, расстояние между ними составило на 300 метров меньше изначального. Каким было изначальное расстояние между лыжниками?
Задача 2. Туристы пошли в похол. На указателе в деревне было написано, что до места назначения осталось 2 часа 55 минут пешим ходом. Из этой деревни они вышли в 12-00. В 13-00 они устроили 15-минутный привал и увидели другой указатель, согласно которому до места назначения остаётся 1 час 15 минут ходьбы пешком. После привала они продолжили путешествие с той же самой скоростью и шли без остановок. В котором часу туристы добрались до места назначения?
Задача 3. В подсобном помещении 2х4 метра устроили ремонт. Вдоль одной из длинных стен по полу был прикреплён 4-метровый короб для проводов шириной 6 см. Оставшуюся площадь пола выложили плиткой. В наличии было два вида квадратной плитки со сторонами x см и y см. Причём длины сторон плиток были целыми сантиметрами. На выкладку пола было потрачено ровно 125 плиток одного вида и ровно 114 плиток другого вида. Назовите все возможные размеры плиток, подходящих под условие.
Задача 6

Задача 3. В подсобном помещении 2х4 метра устроили ремонт. Вдоль одной из длинных стен по полу был прикреплён 4-метровый короб для проводов шириной 6 см. Оставшуюся площадь пола выложили плиткой. В наличии было два вида квадратной плитки со сторонами x см и y см. Причём длины сторон плиток были целыми сантиметрами. На выкладку пола было потрачено ровно 125 плиток одного вида и ровно 114 плиток другого вида. Назовите все возможные размеры плиток, подходящих под условие.
Задача 4. Вычислите
Задача 5
Мастер спорта даёт сеанс одновременной игры в шахматы на нескольких досках. За первые два часа он выиграл P% всех партий и проиграл L партий. За следующие два часа он выиграл Q% остальных партий, M партий проиграл и N партий закончились вничью. Сколько игр сыграл мастер?
Задача 6
Имеются купюры номиналом 1, 10, 100 и 1000 рублей. Сколько существует способов получить миллион рублей из двух тысяч купюр?
Задача 7
К некоторому числу прибавили сумму его цифр. С результатом проделали то же самое. Всего операцию проделали 5 раз и получили 1000. Назовите изначальное число и приведите метод его нахождения, не являющийся грубым перебором.
Задача 8
Формула-1 впервые проводится в Москве , по развязке МКАДА с Рублевкой (картинка в виде 4х кривых клеверных листиков).Осмотрев трассу, гонщик Шухерман представил ее приближенно как сопряжение дуг окружностей и забил в бортовой компьютер следующий закон движения: стараться,чтобы скорость (в футах/сек) была численно равна радиусу проходимой окружности в метрах.. Оцените результат Шухермана на круге (между двумя соседними прохождениями точки старта)

Задача 9
Посади олигарха.Городок имеет форму прямоугольника 4х6 км. Данные слежения за олигархом Жульманом и его автомобилем в течение последней недели:
1.Пробег автомобиля 2517 км.
2.Сумма модулей всех углов поворота стрелки компаса ,закрепленного на приборной панели автомобиля, 2010 румбов (1 румб=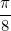 .
.
3.Автомобиль в отсутствие в нем Жульмана не передвигался.
4.Движение задним ходом не применялось.
К сожалению, аппаратуру, снимавшую другие данные, олигарх сумел вывести из строя.
Можно ли на основании этих данных доказать, что Жульман нарушил подписку о невыезде из городка?
Приведите речь эксперта обвинения. если да, и адвоката, если нет. На презумпцию особо не надейтесь.
Задача 1
ОтветитьУдалитьОт момента, когда первый лыжник заехал на сложный участок, до момента, когда второй лыжник заехал на сложный участок, первый ехал со скоростью 12 км/ч x м, а второй - со скоростью 8 км/час х-300 м
V1=12 км/ч=10/3 м/с
V2=8 км/ч=20/9 м/с
S1=x м
S2=x-300 м
t1=t2
x/(10/3)=(x-300)/(20/9)
x=900 м
Ответ: 900 м
щпшлуопкоишщкищуоиоцрищгцурпщгурпокрмгорморургиурогу78п48н938698кшзкпкопшшуокшпокшпо4епкопрцгпрщгрпгщурпшпщуцпхщимбдсьтььвзжаззцъзркщзтшу049н48н8лаогтлкопзщкзщлцрщцгшпкрилцлщпцзцхпцпзщцшец3гзшшепгеее9п0ущпшунр499е8й2-9нп9шцлолцшалзущцплзшцжпуоргщцропгшцрпгшкщупшкрошкршопшеоывапролапоткуыгшфгщцдукалорпфйцукенгшщзфяяывапролдячсмитьбю234567890тиовиоиоаоовокогкгакгпли
УдалитьЗадача 2
ОтветитьУдалитьПервый участок а метров, второй б метров. Время прохождения соответственно 60 мин и х мин. По указателю - 100 мин и 75 мин.
а/60=б/х - скорость хотьбы
а/100=б/75 - скорость по указателю
а=60б/х
(60б/х)/100=б/75
60б/100х=б/75
3/5х=1/75
х=45 мин - время прохождения второго участка
Вышли от привала в 13:15. К месту назначения добрались в 14:00.
Задача 1
ОтветитьУдалитьОтвет: 900 м.
Если я правильно понял условие.
Пусть х - первоначальное расстояние между лыжниками. Тогда х/12=(x-0.3)/8.
Задача 2
ОтветитьУдалитьОтвет: В 14-00.
Туристы идут в 1 2/3 раза быстрее, чем положено. Значит, оставшиеся 75 мин они пройдут за 45 мин.
Nazva получает 5+5+10=20 баллов.
ОтветитьУдалитьSmekalka получает 3+3=6баллов.
Область переходит к Nazv'e, которая должна в течение следующего хода укрепить её задачами
Укрепление 1
ОтветитьУдалить===Условие
В подсобном помещении 2х4 метра устроили ремонт. Вдоль одной из длинных стен по полу был прикреплён 4-метровый короб для проводов шириной 6 см. Оставшуюся площадь пола выложили плиткой. В наличии было два вида квадратной плитки со сторонами x см и y см. Причём длины сторон плиток были целыми сантиметрами. На выкладку пола было потрачено ровно 125 плиток одного вида и ровно 114 плиток другого вида.
Назовите все возможные размеры плиток, подходящих под условие.
===Решение
Площадь помещения = 200х400 см, площадь выложенного пола (200-6)х400=77600 см кв
Площадь использованной плитки = 125x^2+114y^2
125x^2+114y^2=77600
y^2=(77600-125x^2)/114=681-x^2-(34+11x^2)/114
Положим 34+11x^2=114a
x^2=(114a-34)/11=10a-3+(4a-1)/11
Положим 4a-1=11b
a=(11b+1)/4=3b-(b-1)/4
Положим b-1=4c
b=4c+1 подставим в a
a=(11b+1)/4=11c+3 подставим в x^2
x^2=(114a-34)/11=114c+28 подставим в y^2
y^2=(77600-125x^2)/114=650-125c
Из последних выражений получаем 0<=c<=5
Подставив целые значения с в формулы x^2 и y^2 обнаруживаем, что при с=2 x^2=256 y^2=400
Из чего получаем x=16, y=20
Остальные значения с не дают полных квадратов.
Ответ: размеры плиток 16 см и 20 см являются единственно возможными.
x=16
ОтветитьУдалитьy=20
Больше подходящих размеров нет
zhekas получает 5+10=15 баллов и контроль над областью
ОтветитьУдалитьВычислите:
ОтветитьУдалитьhttp://mathurl.com/29bzyd3
Ответ 1340
составляется уравнение
ОтветитьУдалить125*x^2+114*y^2=400*194
первое слагаемое делится на 5 и сумма тоже. тогда и второе слагаемое тоже делится на пять y=5m. Подставляем и сокращаем.
125x^2+114*25*m^2=400*194
5*x^2+114*m^2=16*124
второе слагаемое делится на 2 и сумма тоже. Значит и первое слагаемое делится на 2. x=2n
5*4*n^2+114*m^2=16*194
5*2*n^2+57*m^2=16*97
дальше m=2a
5*2*n^2+57*4*a^2=16*97
5*n^2+57*2*a^2=8*97
n=2b
5*2*b^2+57*a^2=4*97
a=2c
5*b^2+57*2*a^2=2*97
b=2d
5*2*d^2+57*a^2=97
откуда a=1 d=4
x=2*2*2*2=16 y=5*2*2=20
Тут 2 суммы по 670 слагаемых. Слагаемые с одинаковыми номерами дают в сумме 2.
ОтветитьУдалитьСумма равна 2*670=1340
Задача 4
ОтветитьУдалитьПредставим выражение в первых скобках как сумму по n.
Слагаемым будет выражение
((3n-2)+(3n-1))/3n=2-1/n
Количество слагаемых 2010/3=670
Второе выражение имеет вид: сумма по n от 1 до 670 (1/n)
Результат
S=SUM(2-1/n)+SUM(1/n)=SUM(2)-SUM(1/n)+SUM(1/n)=SUM(2)=670*2=1340
Ответ: 1340
Извините, если порчу настроение, но уравнение на количество плиток, примыкающих к меньшей стороне 16m+20n=194 решений не имеет (по делимости на 4), значит и при х=16 у=20 паркета не существует, с учетом поста Zhekas у задачи 3 решений нет
ОтветитьУдалить=1340
ОтветитьУдалитьNazva получает +15 баллов и область
ОтветитьУдалитьE-Science не имела на ходу 5 общей границы
Про предыдущий захват области Zhekas'ом - большое спасибо, ведь и вправду! Мне надо быть внимательнее. Однако тот факт, что один участник дал неправильное решение задачи, совпадающее с правильным решением по мнению другого игрока, оставляет предыдущий захват и очки в силе.
Однако теперь к условиям я отношусь ответственнее, к чему призываю и команды
Джунгли
ОтветитьУдалить===Укрепление 1
Мастер спорта даёт сеанс одновременной игры в шахматы на нескольких досках. За первые два часа он выиграл P% всех партий и проиграл L партий. За следующие два часа он выиграл Q% остальных партий, M партий проиграл и N партий закончились вничью. Сколько игр сыграл мастер?
===Решение
Пусть Х - количество игр.
За первые два часа сыграно игр: X*P/100+L
Следующие два часа: (X-(X*P/100+L))*Q/100+M+N
X=X*P/100+L+(X-(X*P/100+L))*Q/100+M+N
После нехитрых манипуляций получаем
10000*(M+N+L)-100*(Q+L)
Х=-----------------------
10000+P*Q-100*(P+Q)
[надежда на ошибку в манипуляциях]
===Укрепление 2
Имеются купюры номиналом 1, 10, 100 и 1000 рублей. Сколько существует способов получить миллион рублей из двух тысяч купюр?
===Решение Числа 1,10,100,1000 при делении на 9 дают остаток 1. Таким образом сумма купюр даёт такой же остаток, как и их количество.
2000 mod 9 = 2
1000000 mod 9 = 1
Ответ: Невозможно получить миллион из 2000 купюр указанных достоинств (обосновать!).
===Укрепление 3
К некоторому числу прибавили сумму его цифр. С результатом проделали то же самое. Операцию проделали 5 раз и получили 1000. Назовите изначальное число.
===Решение
1) 101x+11y+2z=1000
x=9 -> 11y+2z=1000-909=91
Решаем уравнение, получаем y=2a+1 z=40-11a -> 0 a=3 -> y=7, z=7, x=9 -> 977
2) 11y+2z=977-909=68 -> y=2a z=34-11a -> 0 a=3 -> y=6, z=1, x=9 -> 961
3) 11y+2z=961-909=2 -> y=2a z=26-11a -> 0 a=2 -> y=4, z=4, x=9 -> 944
4) 11y+2z=944-909=35 -> y=2a+1 z=12-11a -> a=1 -> y=3, z=1, x=9 -> 931
5) 11y+2z=931-909=22 -> y=2a z=11-11a -> a=1 -> y=2, z=0, x=9 -> 920
Ответ: 920
Просьба принимать ответ с обоснованием. Обратной проверки недостаточно.
По поводу задачи про плитку: в задаче не сказано, что кладутся целые плитки. Сказано лишь, что использованы целые плитки. Т.е. половинка там, половинка там.
ОтветитьУдалитьПоэтому уравнение 16m+20n=194 не обязано иметь целые решения.
Да-да, я потом на это тоже обратил внимание :)
ОтветитьУдалитьЗадача 5.Находим число партий отдельно по промежуткам,данных хватает.
ОтветитьУдалитьответ S=L/(1-0,01P)+(M+N)/(1-0,01Q)
Да, придется поправиться.
ОтветитьУдалитьЗадача 5. Всего игр:
(L+N+M+Q(N+M)/(100-Q))*100/(100-P)распределение результатов в первом промежутке ведь немного зависит от того, сколько отложено до второго.
Задача 7
ОтветитьУдалитьN5=1000
N4 (число шаг назад) больше 1000-27 но меньше 1000-9-7, итого с 973 до 987 (эти границы можно еще итерационно уточнять, когда не лень).
Делимость на 9: остаток у 1000 =1,значит сумма 2х остатков по 5.Такие у 977=N4 (подходит) и 986 (не подходит)
Остаток 5 может быть только суммой двух остатков по 7 значит у N3 остаток 7. N3 в границах 977-24=953 и 977-9-5=963 тут одно число 961=N3
Делимость N2 на 9- снова выполняем деление на 2 в поле зет-9, остаток у N2 8
Границы: 961-2*9-4=939 и 961-9-3=949 одно число 944=N2
Делимость N1 на 9: остаток 4. Границы: 944-2*9-2=924 и 944-9-1=934 N1=931
Искомое N в границах 931-2*9-1=912 и 931-9=922, остаток у него 2 Тут число
N=920
Проверка
920+11= 931 931+13=944 944+17=961 961+16=977 977+23=1000
6.Пусть x купюр по 1 рублю,
ОтветитьУдалитьy купюр по 10 рублей,
z купюр по 100 рублей,
t купюр по 1000 рублей,
тогда
x + y*10 + z*100 + t*1000 = 1000000
x + y + z + t = 2000
Из первого вычтем 2-ое
9*y + 99*z + 999*t = 998000
Слева на 9 делится, а справа - нет.
Ни одного способа нет.
Ну я и загнул вчера "поле Зет-9",когда и ребенку ясно, что это кольцо.Впрочем, на решение это никак не влияет, ждем оценки наших трудов :)
ОтветитьУдалить"ждем оценки наших трудов"
ОтветитьУдалитьА мы ждём оценки наших не менее вашего )))
Задача 5 - НЕВЕРНО
Задача 6 - ВЕРНО
Задачу 7 оценить тяжело. Ответ-то верный, конечно, но подход к поиску сомнительный. Мой вариант более прост и более очевиден. Оставим оценку этой задачи ведущему.
Честно говоря, в задаче 7 я бы тоже так искал, не вводя переменных. Вполне рациональный подход.
ОтветитьУдалитьE-science получает 5+5=10 баллов.
Назва получает +1 балл
Задача 5 , исправлено после ошибки на пред.ходу
ОтветитьУдалитьВсего было Х партий, за 2 первых часа закончились (X*P/100+L), осталось (X-X*P/100-L) партий, из них выиграно (X-X*P/100-L)*Q/(100-Q), а всего за 2 последних часа сыграно (X-X*P/100-L)*Q/(100-Q)+M+N партий, получаем
((X-X*P/100-L)*Q/(100-Q)+M+N)= (X-X*P/100-L)
Тогда X = (L+(M+N)*100/(100-Q))*100/(100-P)
Повторю пост: Задача 5 , исправлено после ошибки на пред.ходу
ОтветитьУдалитьВсего было Х партий, за 2 первых часа закончились (X*P/100+L), осталось (X-X*P/100-L) партий, из них выиграно (X-X*P/100-L)*Q/(100-Q), а всего за 2 последних часа сыграно (X-X*P/100-L)*Q/(100-Q)+M+N партий, получаем
((X-X*P/100-L)*Q/(100-Q)+M+N)= (X-X*P/100-L)
Тогда X = (L+(M+N)*100/(100-Q))*100/(100-P)
E-science получает 5+10=15 баллов и область
ОтветитьУдалитьКартинку МКАДа поправьте. Она не увеличивается.
ОтветитьУдалитьДа, это просто ошибка на картинке, она и не должна.
ОтветитьУдалитьЗадача 9
ОтветитьУдалитьЗадача 9
Путь по границе городка является "самым прямым", т.е. соотношение 20 км на 2pi (16 румбов) максимально возможное.
Общий пройденный путь равен 2517 км. = 125,85 кругов по границе города.
При таком пути минимально возможный угол 125,85*16=2013,6 румбов
Т.е. путь должен быть ещё более прямым (должно быть меньше поворотов), из чего следует, что был осуществлён выезд за границы города.
Этот комментарий был удален администратором блога.
ОтветитьУдалитьЗадача 8
ОтветитьУдалитьИмеем путь и 4-х дуг одного радиуса и 4-х дуг другого радиуса, построенный по принципу построения овала.
http://img832.imageshack.us/img832/8383/81421286.jpg
Длина дуг равна R1*a1 и R2*a2, где R1 и R2 - радиусы дуг, a1 и a2 - углы дуг.
Время, требуемое на прохождение этих дуг со скоростью, равной радиусу, равно значению угла дуги.
По принципу построения дуг овалов точки сопряжения дуг (В1 и С1) лежат на прямой, проходящей через центры окружностей дуг.
Легко заметить, что 4 таких прямых вместе с осями O1O2 и O1O4 разбивают окружности дуг на 12 равный частей. Равность частей следует из того, что углы наклона этих прямых в вертикальной и горизонтальной оси равны.
Угол одной части равен 2пи/12=пи/6. Дуга меньшего радиуса состоит из 7 частей = 7пи/6, дуга большего радиуса состоит из двух частей = 2пи/6. Всего сумма углов дуг в одной четверти пути составляет 9пи/6=3пи/2.
Сумма углов дуг всего пути составляет 4*3пи/2=6пи.
Ответ: оценочное время прохождения круга = 6пи
Уточнение к задаче 8
ОтветитьУдалитьУчитывая, что 1 фут/сек = 0.3 м/с, то
оценочное время = 6пи/0.3=20пи секунд
Сообщение MagTux 5 ноября 2010 г. 15:43 опуликовал случайно раньше времени. Вот оно:
ОтветитьУдалитьЗадача 9 - поправка Путь по границе городка является "самым прямым", т.е. соотношение 20 км на 2pi (16 румбов) максимально возможное. Общий пройденный путь равен 2517 км. = 125,85 кругов по границе города. Пусть было пройдено 125,5 кругов, что соответствует 2510 км и 2008 румбов. Теперь нужно распределить 7 км и 2 румба. Находясь в вершине границы города и "смотря" на длинную границу можно повернуть на угол atan(6/4)<2 румба, чтобы выехать на диагональ, которая равна sqrt(4^2+6^2)~7.2, чего достаточно для распределения пути внутри города. Оставшиеся половину румба можно "накрутить зигзагами" на пути по диагонали. Такими могут быть доводы адвоката для оправдания олигарха.
Назва получает 5+5=10 баллов
ОтветитьУдалитьE-Science +1 балл за сохранение области
Опечатался в поправке задачи 9
ОтветитьУдалитьНаходясь в вершине границы города и "смотря" на длинную границу можно повернуть на угол atan(4/6)<2 румба, чтобы выехать на диагональ, которая равна sqrt(4^2+6^2)~7.2