
Чтобы занять область, нужно решить 1 задачу:
Задача 7
Найти наибольшее значение выражения
при всевозможных положительных значениях переменных x1, ... xn, либо наилучшую ограничивающую его величину, если наибольшее значение недостижимо.
К карте математического острова
Решенные задачи:
Задача 1. 11 девочек и n мальчиков собрали вместе n2+9n-2 грибов. Все дети нашли грибов поровну. Кого больше: мальчиков или девочек и на сколько?
Задача 2. Сколько решений имеет уравнение |x-|x-|...x-|x-1|...|||=1 (уравнение содержит 2010 модулей)?
Задача 3 Квадрат со стороной 2010 разбит квадратной сеткой единичного шага. Найдите размеры прямоугольника с наибольшей разницей сторон, который в данной сетке встречается миллион раз.
Задача 4
Про натуральное число m известно, что в десятичной записи числа m3 не менее 5 цифр, а в записи числа m8 не более 11 цифр. Сколько цифр в записи числа m24?
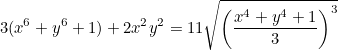
Задача 5
Найти все решения уравнения
Задача 6
В примере несколько цифр заменены звездочками
113*4-1*05=*5*
Верните пример к исходному виду, если известно, что
12013+1345=1328
Также известно, что есть по крайней мере две *, заменяющие одну и ту же цифру
Мальчиков 9 (на 2 меньше, чем девочек).
ОтветитьУдалить(n^2+9n-2)/(11+n): сколько грибов нашёл каждый ребёнок.
В целых числах подходит n=9.
Smekalka получает 5 баллов.
ОтветитьУдалитьДля захвата области остаётся решить всего одну задачу!
Задача 2.
ОтветитьУдалитьПосле раскрытия каждого из модулей кол-во вариантов выражения справа от знака равно увеличивается вдвое.
Ответ. 2^2010 корней.
Um-nik Nazva.net
2) На луче [1,\infty) все модули раскрываются со знаком +. Все x взаимоуничтожаются и остаётся уранение 1=1.
ОтветитьУдалитьПоэтому решениями будет весь луч [1,\infty) и скорее всего ещё что-то.
Ответ: бесконечно много
множество решений имеет мощность континуум
ОтветитьУдалитьЗадача 2
ОтветитьУдалитьРассмотрим выражение
y=|x-|x-1||
Для x=0 -> y=|0-|0-1||=1
Для x=1 -> y=|1-|1-1||=1
Для x>1 (модули можно опустить) -> y=x-(x-1)=1
Т.е. при любом x>=1 y=1
Рассмотрим 4 модуля из выражения:
y=|x-|x-|x-|x-1||||=|x-|x-1||=1
Так как модулей чётное количество, то исходное выражение равно единице при любом x>=1, а также при x=0.
Ответ: бесконечное количество решений.
Задача 1.
ОтветитьУдалитьПосле раскрытия каждого из модулей, кол-во вариантов выражения справа от знака увеличивается вдвое.
Ответ. 2^2010 корней.
На 2м ходу от команды Назвы пришло 2 разных решения. Прошу определиться, какое же решение всё-таки будете использовать для штурма?
ОтветитьУдалитьПринимай моё решение задачи 2.
ОтветитьУдалитьВот теперь контроль над областью перешёл к Назве. Она получает 5+10=15 баллов
ОтветитьУдалить===Условие
ОтветитьУдалитьКвадрат со стороной 2010 разбит квадратной сеткой единичного шага. Найдите размеры прямоугольника с наибольшей разницей сторон, который в данной сетке встречается миллион раз.
Если возьмем 1762Х1, то имеем в строке 2010-1762+1=249 и тогда 2*2010*249=1000980, а вот 1763X1 всего 996960
ОтветитьУдалить===Решение
ОтветитьУдалитьПусть размеры прямоугольника x и y, 0 11
2011-y=500 -> 1511
Ответ: 11х1511 (просьба не принимать ответ без обоснования)
пусть x,y - стороны прямоугольника.
ОтветитьУдалитьтогда сторона x можно поставить по горизонтали 2011-x способами, а y по вертикали 2011-y
2011-x=k
2011-y=1000000/k
x=2011-k
y=2011-1000000/k
x-y=1000000/k-k
функция убывающая. тогда минимум будет в наименьшем k при котором x,y положительны достигается при k=500
x=1511
y=11
Zhekas получает 5+10=15 баллов и область
ОтветитьУдалитьВидя решение E-science понимаю, что условие лучше было бы сформулировать "ровно миллион раз", чтобы избежать неоднозначности
Команда E-science решила задачу с "как минимум миллион раз", сей факт полагаю, можно отметить +5 баллами.
в решении товарища X. Если взять прямоугольник 1762x1, то в квадрате он будет помещаться (2011-1762)*(2011-1)=249*2010=500490 раз, что меньше миллиона
ОтветитьУдалитьРешение товарища X, натолкнуло на то, что прямоугольник можно переворачивать. Тогда разность будет ещё больше. А именно
ОтветитьУдалитьпри x=1761
y=11
разность будет уже 1750. и если прямоуголник можно переворачивать. То тогда он встречается ровно 1000000 раз.
Про натуральное число m известно, что в десятичной записи числа m^3 не менее 5 цифр, а в записи числа m^8 не более 11 цифр. Сколько цифр в записи числа m^24.
ОтветитьУдалитьРешение.
Из первого условия 3lg m >=4
Из второго условия 8lg m <11
Умножая первое неравенство на 8 а второе на 3, получим
32<=24lg m<33
Откуда m^24 состоит из 33 цифр.
Задача 4
ОтветитьУдалитьm^3>=5 цифр
m^3>=10000
m>=21
m^8<=11 цифр
m^3<10^11
m<=23
21^24 имеет 32 знака, 23^24 имеет 33 знака.
Ответ: 32 или 33 знака
Указанным условиям отвечают 2 числа 22 и 23. В 24 степени у них по 33 по 11 цифр.
ОтветитьУдалитьПоправка к решению MagTux:
ОтветитьУдалитьЗадача 4
m^3>=5 цифр
m^3>=10000
m>=22 (а не 21)
m^8<=11 цифр
m^8<10^11
m<=23
22^24 имеет 33 знака, 23^24 имеет 33 знака.
Ответ: 33 знака.
Nazva получает 5+10=15 баллов и контроль над областью
ОтветитьУдалитьА мы что-то в 22.02 написали, что не так?
ОтветитьУдалитьВообще-то, правильный ответ дали E-science:
ОтветитьУдалитьНазва Ответ: 32 или 33 знака
21:44
затем
E-science
22:02
и затем Назва поправка в 0:33
Так что Назва +3 балла, E-science +5+10=15 баллов и область
требуем пояснить условие задачи 6
ОтветитьУдалитьчто такое "если известно, что 12013+1345=1328" ???
Тут математические манёвры, и задачки типа "угадай шифровку" или "что такое чёрное на 3 ногах" здесь не в тему.
(назва)
Задача проверялась на корректность и вполне подходит для маневров. Догадка действительно очень красивая и математическая.
ОтветитьУдалитьГенерал, вы свои же правила нарушили.
ОтветитьУдалитьФормально условие задачи 6 не подходит для манёвров, т.к. тут используется нечто, что не проходят в школе и на первом курсе немат.вузов.
Т.е., школьник или первокур, увидев условие этой задачи, удивлённо ответит: "мы такие странные операции над числами не проходили", и будет прав. ;)
(назва)
ладно, дошло уже...
ОтветитьУдалитьудалите мои 2 (точнее, уже 3) последних коммента
ОтветитьУдалитьМожно зарегаться? ник DMA, цвет фиолетовый если можно
ОтветитьУдалитьможно зарегаться? ник DMA. форма личная , цвет фиолетовый если можно
ОтветитьУдалитьблин комп глючит
ОтветитьУдалитьЕсть решение 6 задачи правда примитивное какое то получилось.
ОтветитьУдалитьDMA, построить таблицу сложения, по которой было бы верно равенство 12013+1345=1328 - интересный подход. Однако выведенный вами набор правил - не единственен, удовлетворяющий этому выражению, к примеру, вы не рассматриваете возможность, что где-то происходил перенос.
ОтветитьУдалитьтак что пока крепость устояла
Берег уравнений, задача 5
ОтветитьУдалитьКрасивого решения не нашёл, зато задача решается без всяких хитростей с применением матанализа.
Перепишем уравнение в однородном виде, введя дополнительную переменную и сократив степени переменных в два раза
http://mathurl.com/2549fyh.png
Доказав, что это уравнение не имеет других неотрицательных решений кроме случая, когда x=y=z, мы автоматически докажем, что у исходного уравнения нет других решений кроме (1,1), (-1,1), (1,-1), (-1,-1)
Поскольку уравнение однородное, мы можем как нам удобно нормировать тройку переменных (x,y,z). Например, будем рассматривать только тройки чисел, лежащие на сфере радиуса sqrt(3), чтобы правая часть уравнения превратилась в константу 11. Утверждается, что левая часть уравнения равна 11 при x=y=z и строго больше 11 во всех остальных точках куска сферы, лежащего в области x,y,z > 0.
Легко проверить, что на границе этого куска сферы, т.е., там, где две переменных из трёх нули, левая часть строго больше правой. Осталось убедиться, что на внутренних точках этого куска сферы нет локальных минимумов меньше 11. Это типичная задача на поиск условного экстремума, решаемая методом множителей Лагранжа. Система уравнений становится такой:
http://mathurl.com/24m5x8c.png
Т.к. график функции A*X+B/(X^2) не может пересекать горизонтальную прямую более чем в друх точках при положительных X, то второе (сдвоенное) уравнение системы означает, что как минимум две из трёх переменных x,y,z имеют одинаковое значение.
Отсюда 4 случая:
1) x=y=z
2) x=2/sqrt(34), y=z=7/sqrt(34)
3) y=2/sqrt(34), x=z=7/sqrt(34)
4) z=2/sqrt(34), x=y=7/sqrt(34)
С первым случаем всё и так ясно, а в остальных трёх случаях значение левой части уравнения будет примерно 11.5, что нас вполне устраивает. :)
(назва)
дополнение к решению задачи 5
ОтветитьУдалитьтам неполностью рассмотрен случай границ куска сферы - когда одна переменная 0, а две другие не 0.
в этом случае вместо сферы - окружность
x^2+y^2=3
и нужно доказать, что
3*(x^3+y^3) > 11
доказывается так:
x^3+y^3 = (x^2+xy+y^2)*(x+y) = (3+xy)*sqrt(3+2xy)
это больше или равно чем
3*sqrt(3) > 11/3
(назва)
согласен, а это материал примерно какого класса
ОтветитьУдалитьDMA
Ничего выходящего за пределы школьных понятий, как и другие задачи Маневров
ОтветитьУдалитьНазва получает 5 баллов
ОтветитьУдалитьE-Science +1 балл за сохранение области
Задача 6
ОтветитьУдалитьПоследние цифры чисел - это основа системы счисления.
12013+1345=1328
При переводе в десятичную получаем:
46+44=90
Теперь подбираем варианты для примера
113*4-1*05=*5*
Первая звёздочка может заменять цифры 0-3, вторая - 0-4, третья - 0-9, четвёртая 6-9.
Равенство выполняется при:
11304-1405=657
11314-1005=759
11314-1305=658
11324-1205=659
11334-1405=559
Условие равности двух звёзд выполняется только при
11324-1205=659
Ну вот, раскрылась-таки шифровка :)
ОтветитьУдалитьНазва +5, E-science +1