ММ130
Комната имеет форму прямоугольного параллелепипеда шириной
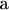 , высотой
, высотой 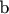 и длиной
и длиной  . На стене
. На стене 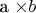 сидит таракан. Он находится на расстоянии
сидит таракан. Он находится на расстоянии 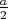 от смежной стены и на расстоянии
от смежной стены и на расстоянии 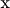 от потолка,
от потолка, 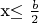 и хочет попасть в точку, симметричную исходной относительно центра параллелепипеда.
и хочет попасть в точку, симметричную исходной относительно центра параллелепипеда.Для некоторых значений
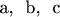 кратчайший путь между этими точками будет проходить через одну и ту же последовательность граней при любом x,
кратчайший путь между этими точками будет проходить через одну и ту же последовательность граней при любом x, 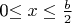 . Для каждой такой последовательности граней приведите пример тройки
. Для каждой такой последовательности граней приведите пример тройки 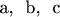 .
.Примечание: термин "кратчайший путь" означает путь, для которого нельзя найти путь, более короткий.
====================================
Решение
Приведём в основном решение Сергея Половинкина
Пронумеруем стороны данного прямоугольного параллелепипеда.
Грань, на которой сидит таракан, обозначим 1, боковую грань слева от 1-ой (стена) - грань 2, снизу (пол комнаты) - грань 3, правая боковая стена - грань 4, сверху (потолок комнаты) - грань 5, задняя стенка, та, куда держит путь таракан, грань 6.
Обозначим каждую грань соответствующим цветом:
1. сиреневый
2. розовый
3. голубой
4. зеленый
5. желтый
6. бирюзовый
Рассмотрим различные маршруты между заданными точками по граням параллелепипеда. Любой маршрут начинается на грани 1, а заканчивается - на 6.
Очевидно, что любой кратчайший путь (КП) не может включать одну и ту же грань дважды. Кроме того, понятно, что любой КП представляет из себя отрезок прямой, соединяющий 2 заданные точки на некоей развертке параллелепипеда.
Рассмотрим "обобщенную" развертку:

На этом рисунке при разничных значениях параметров a, b, c можно нарисовать все КП, проходящие через боковые грани 2 и 4. Также приведено несколько прямых маршрутов, которые при соответствующих значениях a, b, c, x, возможно, могут быть КП:
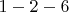 ,
, 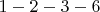 ,
, 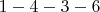 .
.На следующем рисунке показаны маршруты через пол и потолок:

На рисунке приведены маршруты (потенциальные КП)
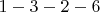 ,
, 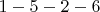 ,
, 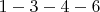 ,
, 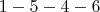 .
.А на следующем рисунке можно построить все маршруты, которые теоретически могут быть КП.

Такие маршруты могут включать в себя
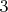 ,
, 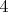 или
или 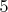 граней, но не
граней, но не 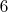 , все начинаются с
, все начинаются с 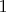 и заканчиваются в
и заканчиваются в 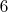 , остальные грани входят не более одного раза. Всего имеем
, остальные грани входят не более одного раза. Всего имеем 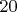 таких маршрутов, ввиду симметрии, их длины равны попарно, всего имеем
таких маршрутов, ввиду симметрии, их длины равны попарно, всего имеем 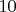 пар, найдем длины всех
пар, найдем длины всех 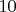 :
:1.
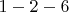 и
и 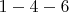 , длина
, длина 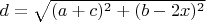
2.
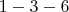 и
и 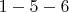 , длина
, длина 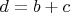
3.
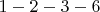 и
и 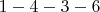 , длина
, длина 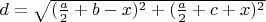
4.
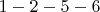 и
и 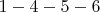 , длина
, длина 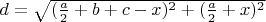
5.
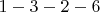 и
и 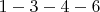 , длина
, длина 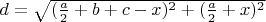
6.
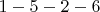 и
и 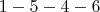 , длина
, длина 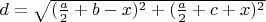
7.
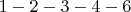 и
и 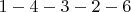 , длина
, длина 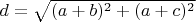
8.
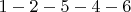 и
и 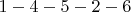 , длина
, длина 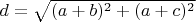
9.
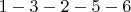 и
и 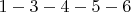 , длина
, длина 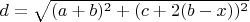
10.
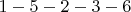 и
и 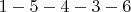 , длина
, длина 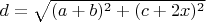
Заметим, что длины маршрутов 3 и 6 равны, также равны маршруты 4 и 5.
Для любого набора параметров a, b, c и при любом допустимом значении x длины маршрутов 7 и 8 больше длины маршрута 1, а маршрута 9 - больше длины маршрута 2.
Получаем 5 маршрутов:
M1:
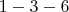 и
и 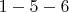 , длина
, длина 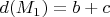
M2:
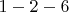 и
и 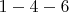 , длина
, длина 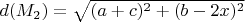
M3:
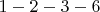 ,
, 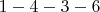 ,
, 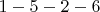 и
и 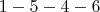 , длина
, длина 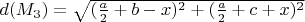
M4:
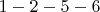 ,
, 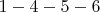 ,
, 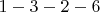 и
и 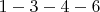 , длина
, длина 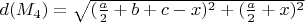
M5:
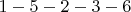 и
и 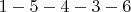 , длина
, длина 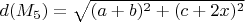
Некоторые из этих маршрутов не существуют при некоторых значениях a, b, c, x, но при других значениях любой из этих 5 может оказаться самым коротким, поэтому нужно рассматривать их все. Кроме того, если маршрут не существует (для какого-либо набора значений), то это означает, что есть другой, более короткий маршрут.
При сравнении длин маршрутов проще сравнивать квадраты длин, что не меняет знака отношения.
Заметим, что при
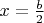 , независимо от значений a, b и c,
, независимо от значений a, b и c, 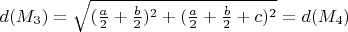 , а при
, а при 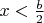 ,
, 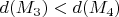 .
.При этом же значении x,
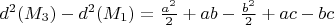 , а
, а 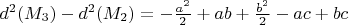 . Эти две величины не могут быть отрицательными одновременно, поэтому маршрут M3 не может быть решением задачи
. Эти две величины не могут быть отрицательными одновременно, поэтому маршрут M3 не может быть решением задачиТеперь, при
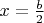 ,
, 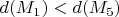 , также независимо от значений a, b и c, тогда М5 тоже не решение задачи.
, также независимо от значений a, b и c, тогда М5 тоже не решение задачи.Маршруты М1 и М2 являются решением, соответствующие значения параметров несложно подобрать.
Например, при
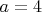 ,
, 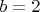 ,
, 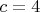 , при всех
, при всех 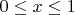 , КП будут только М1.
, КП будут только М1.А при
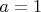 ,
, 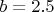 ,
, 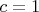 , при любых
, при любых 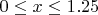 , КП будет M2.
, КП будет M2.Обсуждение
Когда-то прочитал в "Кванте" задачу про насекомого, сидящего почти под потолком на торцевой стене длинного зала. Чтобы попасть в центрально-симметричную точку зала кратчайшим путём ему нужно было пройти по потолку, затем перебраться на боковую стену, затем - на пол, а уже оттуда - на противоположный торец. Придумывая задачу для Марафона я вспомнил о ней, и сначала захотел обобщить - вывести для измерений комнаты a, b, c и координат таракана x и y правила определения длины кратчайшего пути. Затем, в процессе обкатки формулировки y превратилось в
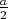 , x стало принимать значения от 0 до
, x стало принимать значения от 0 до 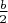 , но рассмотрение всех вариантов всё равно оставалось достаточно объёмным, и первоначальный интерес от поиска маршрутов сменился скукой рутинных вычислений.
, но рассмотрение всех вариантов всё равно оставалось достаточно объёмным, и первоначальный интерес от поиска маршрутов сменился скукой рутинных вычислений. Последовала очередная переформулировка: меня заинтересовало, а найдутся ли такие комнаты, для которых кратчайший маршрут будет проходить всегда черед один и тот же набор граней? В таком виде процесс отсечения неподходящих вариантов необременителен, и задача была включена в Марафон.
Вот только в своём решении я отсекал маршрут
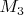 просто на том основании, что существует маршрут равной длины, симметричный ему относительно вертикальной плоскости, проходящей через исходную точку, и, таким образом,
просто на том основании, что существует маршрут равной длины, симметричный ему относительно вертикальной плоскости, проходящей через исходную точку, и, таким образом, 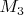 не будет кратчайшим маршрутом в понимании "имеющий длину меньшую, нежели какой-либо другой". Но Алексей Волошин и Анатолий Казмерчук справедливо указали в уточняющих условие письмах, что для любого маршрута найдётся равный ему симметричный относительно центра параллелепипеда. Таким образом в формулировку внесено уточнение, а Алексей Волошин и Анатолий Казмерчук получают +1 балл.
не будет кратчайшим маршрутом в понимании "имеющий длину меньшую, нежели какой-либо другой". Но Алексей Волошин и Анатолий Казмерчук справедливо указали в уточняющих условие письмах, что для любого маршрута найдётся равный ему симметричный относительно центра параллелепипеда. Таким образом в формулировку внесено уточнение, а Алексей Волошин и Анатолий Казмерчук получают +1 балл.Решением задачи в её марафонной постановке являются 2 различных параллелепипеда, представляющие 2 наиболее очевидных маршрута: через потолок и через боковую стену. Это, в общем-то, несколько скучно. Жаль, что я не установил ограничения для x, к примеру,
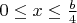 - в этом случае среди решений был бы параллелепипед, кратчайший маршрут в котором проходил бы через 5 граней (возможность того, что такой вариант может быть кратчайшим даже не рассматривалась некоторыми участниками).
- в этом случае среди решений был бы параллелепипед, кратчайший маршрут в котором проходил бы через 5 граней (возможность того, что такой вариант может быть кратчайшим даже не рассматривалась некоторыми участниками).Вот зависимость длины маршрутов для случая
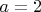 ,
, 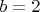 ,
, 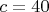 , найденного Сергеем Половинкиным в развитие темы.
, найденного Сергеем Половинкиным в развитие темы. 
Полагаю, это можно отметить дополнительным баллом.
Награды
За правильное решение задачи Сергей Половинкин и Алексей Волошин получают 6+1=7 баллов, Анатолий Казмерчук получает 5+1=6 баллов, Николай Дерюгин и Евгений Гужавин получают по 3 балла.
Эстетическая оценка задачи 4.3 балла
====================================
Разбор задачи ММ130 подготовил Алексей Извалов
Комментариев нет:
Отправить комментарий