
Область на 12 ходу заняла Назва. Возводятся укрепления.
К карте математического острова
Решённые задачи:
Задача 1. Равнобедренный треугольник, ромб и квадрат имеют равную площадь. Основание треугольника равно стороне квадрата и меньшей диагонали ромба. Расположите периметры этих фигур в порядке возрастания
Задача 2. Квадратный лист бумаги со стороной 10см согнули так, что одна его вершина попала на сторону, не смежную с ней. Найдите с точностью до 0, 1 мм такое положение этой вершины, чтобы площадь фигуры, покрытой двумя слоями бумаги была минимальной
Задача 3
У произвольно расположенного на плоскости квадрата на четырех его сторонах отметили точки M,N,K,P, потом сам квадрат стерли. Восстановить квадрат.
Задача 4
У прямоугольного треугольника с катетами 3 и 4 найти расстояние между точкой пересечения биссектрис и точкой пересечения медиан.
Задача 5
Точки D и Е расположены на стороне АС треугольника АВС. Прямые ВD и ВЕ разбивают медиану АМ треугольника АВС на три равных отрезка. Найдите площадь треугольника DEB, если площадь треугольника АВС равна 1.
Чтобы занять область, нужно решить 3 задачи:
Задача 6
Необходимо с помощью циркуля и линейки построить крест, равный по площади фигуре месяца. Крест - обычный, из пяти равных квадратов. Месяц представляет из себя фигуру, вырезанную из меньшей окружности большей как показано на рисунке.
Диаметры окружностей относятся как 1 к корню из двух
Задача 7
Имеется куб со стороной 3 и плоскость-нож, которой можно отделять части куба, проводя разрез в этой плоскости. Чтобы разделить куб на 27 единичных кубиков, не сдвигая его с места, очевидно потребуется 6 разрезов. Найти минимальное количество разрезов (необходимых для разделения куба на 27 единичных), если учесть, что после каждого можно менять расположение частей в пространстве.
Задача 8
Набор белых шахмат привычно выстроился на поле боя... а черных фигур нет!
Пока противник опаздывает, у вас есть 21 ход, чтобы поставить под бой как можно больше пустых клеток. Напишите последовательность своих ходов и докажите, что количество атакованых вами пустых клеток (на момент после 21 хода) максимальное, которого можно достичь за это время.
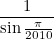
Задача 9
Шириной многоугольника называется максимум расстояний между его произвольными точками. Правильный 2010-угольник со сторонами, равными 1, имеет ширину
Привести пример 2010-угольника со сторонами, равными 1, имеющего ширину еще меньше.
Задача 10
Из шахматной доски 8*8 вырезано с углов по квадрату 2*2.Король обошел оставшиеся клетки по замкнутой ломаной без самопересечений, побывав в центре каждой 1 раз. Какова наибольшая длина его пути, если принять сторону клетки за 1
Задача 11
Разрезать правильный шестиугольник отрезками прямых на 6 частей, из которых сложить правильный треугольник той же площади



Задача 1
ОтветитьУдалитьПериметры в порядке возрастания: треугольник, ромб, квадрат.
Если обозначить сторону квадрата за х, периметры квадрата, треугольника и ромба будут соответственно 4x, x+2√(4x^2+x^2/4), 4√(x^2+x^2/4). Подставляем вместо х единицу, сравниваем результаты (4, 5.12, 4.47 для квадрата, треугольника и ромба).
Задача 1
ОтветитьУдалитьПусть а - сторона квадрата. Площадь квадрата = а^2. Периметр квадрата 4а.
Пусть b - сторона ромба, d - вторая диагональ ромба.
Площадь ромба a*d/2 равна площади квадрата: a*d/2=а^2 -> d=2a
Рассмотрим прямоугольный треугольник, который является общим для половины квадрата и ромба.
b^2=a^2+(a/2)^2 -> b=a/2*корень(5)
Периметр ромба = 4*a/2*корень(5)=2a*корень(5) ~ 4.47a больше периметра квадрата.
Пусть с - боковая сторона треугольника. По Герону площадь треугольника
1/2а*корень(c^2-(a/2)^2) равна площади квадрата
1/2а*корень(c^2-(a/2)^2)=a^2 -> c=а/2*корень(17)
Периметр треугольника = а+2*а/2*корень(17)=a*(1+корень(17)) ~ 5.12a больше периметра квадрата и ромба.
Ответ: квадрат, ромб, треугольник
можэ я где-то ошибся, в общем в 1 задачке такой ответ получился:
ОтветитьУдалитьКвадрат: 4x
Ромб: 4sqrt(x^2+0.25x)
Треугольник: 2(4x^2+0.25x^2)+x
Smekalka получает 5 баллов, Nazva получает 3 балла
ОтветитьУдалитьДля захвата области достаточно решить всего одну задачу!
Задача 2
ОтветитьУдалитьМинимальная площадь будет в случае, когда угол вершины, которая лежит на стороне, образует с этой стороной 45 град (два равнобедренных прямоугольных треугольника).
Из одного такого треугольника имеем:
x^2+x^2=(10-x)^2
x=10/(1*корень(2))~4.142 см
Т.е. вершина угла делит сторону на отрезки 41.42 мм и 58.58 мм.
2) 4.4936
ОтветитьУдалитьКрепость выдержала штурм
ОтветитьУдалитьа у меня правильное решение? (чтоб не мучаться)
ОтветитьУдалитьМинимум находится только численно, х=4,5, еще точнее х=4,494 выражение оптимизируемой функции черех х могу прислать
ОтветитьУдалитьплощадь фигур, которые не накрываются при изгибе, вычисляется по формуле
ОтветитьУдалитьS(x)=(3000x-300x^2+10x^3-x^4)/(10(10+x)), где x положение вершины на не смежной вершине. Дальше ищем производную.
Получается дробь, числитель которой является многочленом четвёртой степени. Приравниваем его к нулю.
Так как не надо получить точный ответ, то я решал данное уравнение делением отрезка пополам.
В итоге x=4.493655
прилагаю схематичный рисунок
ОтветитьУдалитьhttp://i002.radikal.ru/1010/9f/22bed26a0949.png
E-science получает 5+10=15 баллов и область (сама формула присылалась в ЛС на форуме)
ОтветитьУдалитьzhekas получает 3 балла
Задача 3
ОтветитьУдалитьhttp://img688.imageshack.us/img688/1746/101025.jpg
Соединим точки MNKP. На двух противоположных сторонах четырёхугольника MN и KP начертим окружности, диаметром которых являются эти стороны. К сторонам MN и KP через центры окружностей (середины MN и KP) проведём перпендикуляры. Отметим внутри MNKP точки пересечения перпендикуляров с окружностями D1 и D2. На прямой D1D2 лежит диагональ квадрата, причём вершинами квадрата являются точки пересечения диагонали с окружностями. Получили две вершины квадрата А и С. Проводим прямые АК, АР, CN, CM. Фигура, ограниченная этими прямыми - искомый квадрат.
Замечание: не во всех случаях удаётся восстановить квадрат. Например, когда MK и NP перпендикулярны.
Задача 4
Положим треугольник вершиной прямого угла в центр координат, а катетами на оси координат.
Точка пересечения биссектрис - инцентр - центр вписанной окружности. Радиус окружности = (3+4-5)/2=1
Координаты точки пересечения биссектрис (1;1)
Найдём координаты точки пересечения медиан.
Координаты середины меньшего катета = (3/2;0), большего катета = (0;2)
Уравнение медианы к меньшему катету 3y+8x-12=0, к большему 3y+2x-6=0
Точка их пересечения (из системы уравнений) = (1;4/3)
Расстояние между точками пересечения биссектрис (1;1) и медиан (1;4/3) = 4/3-1 = 1/3
Задача 5
Пусть К - точка пересечения BD и AM.
Применим теорему Менелая к треугольнику BCD и прямой АМ
BK/KD*DA/AC*CM/MB=1
BK/KD*DA/AC=1
BK/KD=AC/DA
Применим теорему к треугольнику ВКМ и прямой АС
СМ/СВ*АК/АМ*DB/DK=1
1/2*1/3*DB/DK=1
DB/DK=6 -> BK/KD=5 -> AC/DA=5
Т.о. S(ABD)=1/5, S(CBE)=1/2 -> S(DEB)=1-1/5-1/2=3/10
5)
ОтветитьУдалить0.3
(назва)
Назва получает +25 баллов и область
ОтветитьУдалить[b] Задача 7 [/b]
ОтветитьУдалитьИмеется куб со стороной 3 и плоскость-нож, которой можно отделять части куба, проводя разрез в этой плоскости. Чтобы разделить куб на 27 "единичных" кубиков (со тороной 1), не сдвигая его с места, очевидно потребуется 6 разрезов. Найти минимальное количество разрезов (необходимых для разделения куба на 27 единичных), если учесть, что после каждого можно менять расположение частей в пространстве.
Ответ: Все равно потребуется 6 разрезов. Доказательство: "Внутренний" кубик соприкасается с другими всеми шестью гранями. Никакие две из них не лежат в одной плоскости, а значит, чтобы "освободить" его, потребуется не меньше 6 разрезов, как бы мы не располагали остальные части.
[b]Задача 8[/b]
ОтветитьУдалитьНабор белых шахмат привычно выстроился на поле боя... а черных фигур нет!
Пока противник опаздывает, у вас есть 21 ход, чтобы поставить под бой как можно больше пустых клеток. Напишите последовательность своих ходов и докажите, что количество атакованых вами пустых клеток (на момент после 21 хода) максимальное, которого можно достичь за это время.
Ответ: белые пешки на вертикалях b, d, e и g (королевские и каталонские) доходят до восьмой горизонтали, становясь ферзями. Это 4*5=20 ходов. 21м ходом "свой" ферзь ходит Фd1-d5. Таким образом, атакованы все клетки доски, кроме a1 и c2, но они не пустые (ладья и гамбитная пешка).
[b]Задача 8[/b]
ОтветитьУдалитьНабор белых шахмат привычно выстроился на поле боя... а черных фигур нет!
Пока противник опаздывает, у вас есть 21 ход, чтобы поставить под бой как можно больше пустых клеток. Напишите последовательность своих ходов и докажите, что количество атакованых вами пустых клеток (на момент после 21 хода) максимальное, которого можно достичь за это время.
Ответ: белые пешки на вертикалях b, d, e и g (королевские и каталонские) доходят до восьмой горизонтали, становясь ферзями. Это 4*5=20 ходов. 21м ходом "свой" ферзь ходит Фd1-d5. Таким образом, атакованы все клетки доски, кроме a1 и c2, но они не пустые (ладья и гамбитная пешка).
8.Возможно, в условиях задачи допущена ошибка. Видимо, забыли добавить - без превращения фигур.
ОтветитьУдалитьНо сейчас такая формулировка, вот возможное решение
1. a4 2. a5 3. a6 4. a7 5. a8Ф 6. h4 7. h5 8. h6 9. h7 10. h8Ф 11. d4 12. d5 13. d6 14. d7 15. d8Ф 16. Фa7 17. Фh6 18. Лa5 19. Лh4 и все пустые клетки атакованы. Если нужно ровно 21 ход, то можно добавить еще 2 хода, туда-сюда и снова все пустые клетки атакованы.
Задача 6. Площадь полумесяца S=Пr^2/2+R^2/2-ПR^2/4=R^2/2= 5a^2 ,где а – сторона квадратика из креста
ОтветитьУдалитьПри построении:
1.соединим рога А и В полумесяца отрезком(диаметр меньшей окружности)
2.Нарисуем срединный перпендикуляр к нему
3.Найдем центр большей окружности и проведем радиусы ОА,ОВ=R
4. Построим параллельным проектированием с одной стороны произвольного острого угла на другуюотрезки R/5 и R/2
5.Сложим из них гипотенузу,тогда высота прямоугольного треугольника, падающая в их общую точку, будет R/(корень10)=а = стороне одного из квадратиков креста. Дальше ясно
Задача 7.6 разрезов останется необходимо
угловые единичные кубики имеют по 3 грани совпадающие с внешними гранями большого куба и по 3 грани с соседними единичными кубиками. Для их отделения достаточно 3-х разрезов.
Реберные кубики (не угловые) - 2 внешних и 4, где они соседствуют с 4 единичными кубиками, но еще не разрезаны. За один разрез сразу 2 такие грани не прорезать, т.е. для них надо 4 разреза минимум.
Для граневых (не реберных) кубиков необходимо не менее 5 разрезов.
А для центрального кубика, имеющего 6 соседей, надо не менее 6 разрезов.
8ю уже постили
Задача 8:
ОтветитьУдалитьУсловие действительно следовало бы сделать строже.
Но это мой прокол, а не ваш, задача решена:)
Задача 7:
ОтветитьУдалитьДа.
А мы и с запретом превращений сделали.1. a2-a4 2. a4-a5 3. a5-a6 4. a6-a7 5. Л.a1-a6 6. K.g1-h3
ОтветитьУдалить7. e2-e3 8. Ф.d1-h5 9. C.f1-d3 10 . f2-f4 11. Kp.e1-f2 12. K.b1-c3 13. b2-b4 14. C.c1-b2 15. Л.h1-a1 16. Kp.f2-f1 17. K.h3-f2 18. Ф.h5-h8
19. Л.a6-b6 20. Л.b6-b7 21. Л.a1-a6
Молодцы!
ОтветитьУдалитьвы, правда, оставили без боя клетку h1 (ведь вы ее освободили), но с этим тоже легко справиться.
X2
ОтветитьУдалитьКлетку h1 бьет конь с f2, там все бьется!
а, ну да, просмотрел. Молодцы! Зачет с большой буквы.
ОтветитьУдалитьЗадача 6:
ОтветитьУдалитьЯ понял, что вы вычли из меньшего полукруга
ПR^2/4-R^2/2. А откуда следует, что тот кусочек равен этой разнице?
Lew:'Я понял, что вы вычли из меньшего полукруга
ОтветитьУдалитьПR^2/4-R^2/2. А откуда следует, что тот кусочек равен этой разнице?'
Порядок слагаемых сделан такой, чтобы поняли иначе. Первые два слагаемых в сумме -это площадь криволинейного треугольника АВО,охватывающего и полумесяц.А вычитается уже площадь прямоугольнлго сектора большого круга. Остается полумесяц.
Задача 6:
ОтветитьУдалитьВерно.
Но мое решение проще и красивее:Р
E-science получает 5+5+5+10 баллов и область
ОтветитьУдалитьЗадача 9
ОтветитьУдалитьУ правильного многоугольника с чётным количеством сторон каждая сторона параллельна противоположной ей стороне относительно центра многоугольника. Если на паре противоположных сторон построить прямоугольник, то шириной многоугольника будет диагональ этого прямоугольника. В правильном 2010-угольнике эта диагональ со стороной прямоугольника образует угол pi/2010. Таким образом длина диагонали при стороне 1 равна
x=1/sin(pi/2010), а не 2/sin(pi/2010), как даётся в условии (может я условие понял неверно?)
Угол правильного 2010-угольника равен 2008pi/2010, т.е. развёрнутый угол без 2pi/2010.
Если соединить вершины многоугольника через одну и отразить оставшиеся вершины относительно этих отрезков, то получим правильную 1005-конечную звезду, внешние углы которой равны 2012pi/2010. При этом ширина многоугольника не изменилась. Теперь если увеличивать внешние углы, то звезда будет "стягиваться" к центру и в пределе будет иметь ширину, равную двум сторонам = 2.
http://img257.imageshack.us/img257/9261/10650593.jpg
Ответ: удовлетворяющим условие 2010-угольником будет любая 1005-конечная правильная звезда с внешними углами > 2012pi/2010.
Задача 10
Прямой путь равен 1, путь по диагонали равен sqrt(2).
Поскольку клеток осталось 64-4*4=48, то очевидно, что длина пути будет больше 48.
Граничных полей на доске 28. Поскольку путь не самопересекающийся, то каждый выход на граничную клетку должен быть рядом с предыдущим выходом. У соседних граничных клеток цвета различны, за исключением 4-х углов. Для перехода на другой цвет требуется прямой путь длиной 1. Следовательно таких путей всего должно быть не менее 24. таким образом длиннейший путь равен 24+24*sqrt(2).
В доказательство существования такого пути привожу пример
http://img574.imageshack.us/img574/9596/98301660.jpg
Ответ: 24+24*sqrt(2)
Задача 11
http://img560.imageshack.us/img560/5546/48976098.jpg
Поправка к задаче 10
ОтветитьУдалитьГраничных полей на доске 24. Поскольку путь не самопересекающийся, то каждый выход на граничную клетку должен быть рядом с предыдущим выходом. У соседних граничных клеток цвета различны, за исключением 4-х углов, где возможен переход по диагонали. Для перехода на другой цвет требуется прямой путь длиной 1. Следовательно таких путей всего должно быть не менее 24-4=20.
Разделим доску пополам диагональю целой доски. Легко посчитать, что количество диагональных переходов между двумя половинами равно 9-ти. Т.е. только при диагональных переходах невозможно замкнуть путь. Тогда потребуется ещё один прямой. То же самое и по второй диагонали.
Следовательно прямых путей всего должно быть не менее 22.
Таким образом длиннейший путь равен 22+26*sqrt(2).
Вот пример с 26 диагоналями.
ОтветитьУдалитьhttp://img130.imageshack.us/img130/8198/74803857.jpg
Задача про Короля спасла область
ОтветитьУдалитьНазва получает 5+5=10 баллов
E-Science +1 балл за сохранение области
Клеток осталось 64-4*4=48, т.е. путь состоит из 48 шагов по прямой или диагонали. Прямой путь равен 1, путь по диагонали равен sqrt(2).
ОтветитьУдалитьГраничных полей на доске 24. Поскольку путь не самопересекающийся, то каждый выход на граничную клетку должен быть рядом с предыдущим выходом. У соседних граничных клеток цвета различны, за исключением 4-х углов, где возможен переход по диагонали. Для перехода на другой цвет требуется прямой путь длиной 1. Следовательно таких путей всего должно быть не менее 20. Длиннейший путь равен 20+28*sqrt(2).
http://img573.imageshack.us/img573/8109/72012363.png
Nazva получает 5+10=15 баллов
ОтветитьУдалитьвнутри квадрата со стороной 10 отметили 6 точек, все попарные расстояния целые числа. Доказать, что найдутся равные расстояния. Помогите доказать
ОтветитьУдалитьзнаю точно, решается по принципу Дирихле, если решу, то напишу решение. А так вряд ли кто вам здесь решит эту задачу.
Удалить