
Чтобы занять область, нужно решить задачу:
Задача 8
Про функцию c1+c22x+c33x+...+c20102010x известно, что она обращается в 0 при 2010 различных значениях х. Найти коэффициенты c1,...,c2010
К карте математического острова
Решенные задачи:
Задача 1. Для функции f(x), определённой для всех ненулевых аргументов, выполняется yf(xy)=f(x) для любых x, y из её области определения. Если f(30)=20, то чему равно f(40)?
Задача 2. Виталик сложил числа дней и числа месяцев дат рождения всех своих друзей и получил 35. Даты рождения его друзей различны. Какое наибольшее возможное количество друзей у Виталика?
Задача 3
A,B,C,D - последовательные вершины правильного семиугольника со стороной a. X - точка пересечения AC и BD. AX=b. Найти AD (и записать в максимально короткой форме)
Задача 4
Бильярдист из бильярдных шаров выложил квадрат, а потом из этих же шаров выложил равносторонний треугольник. Количество шаров в стороне квадрата и треугольника отличаются на 2. Сколько у бильярдиста было шаров?
Задача 5
У каждого из чисел от 1 до 999999 посчитали суммы цифр. В получившемся ряду опять посчитали суммы цифр. И т.д. пока в ряду не остались только однозначные числа. Получившиеся числа соединили в 999999-значное число и разделили на 9. Чему равен результат?
Задача 6
Назовём прямоугольный параллелепипед хорошим, если его можно разрезать на два равных прямоугольных параллелепипеда. Сколько существует хороших прямоугольных параллелепипедов, имеющих грань 2x6?
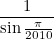
Задача 7
Найти предел при n, стремящемся к бесконечности, последовательности 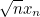
где x0=a, xn=sin xn-1
Задача 9
Шириной многоугольника называется максимум расстояний между его произвольными точками. Правильный 2010-угольник со сторонами, равными 1, имеет ширину
Привести пример выпуклого 2010-угольника со сторонами, равными 1, имеющего ширину еще меньше.

Этот комментарий был удален администратором блога.
ОтветитьУдалитьЭтот комментарий был удален администратором блога.
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьИ тут Назва исопльзовала авиадесант, а я проглядел :)
ОтветитьУдалитьДля соблюдения принципа равных шансов, перепошлите, пожалуйста, решения задач.
ОтветитьУдалитьf(40)=f(30*4/3)=f(30)/(4/3)=20*3/4=15
ОтветитьУдалитьЗадача 2
ОтветитьУдалитьОтвет: 9 [1.1, 1.2, 2.1, 1.3, 2.2, 3.1, 1.4, 2.3, 3.2]
Задача №1
ОтветитьУдалить(3/4)*f(40*(3/4))=f(40);
3/4*f(30)=f(40);
f(40)=3/4*20=15.
Задача №2
9 друзей. Даты: 1.1; 1.2; 2.1; 1.3; 2.2; 3.1; 1.4; 2.3; 3.2.
Nazva получает 5+5+10=20 баллов.
ОтветитьУдалитьzhekas получает 3+3=6баллов.
Область переходит к Nazv'e, которая должна в течение следующего хода укрепить её задачами
Укрепление для функциональных равнин
ОтветитьУдалить===Условие
http://img155.imageshack.us/img155/4595/30962164.gif
A,B,C,D - последовательные вершины правильного семиугольника со стороной a. X - точка пересечения AC и BD. AX=b. Найти AD (максимально короткую форму записи).
===Решение
В правильном семиугольнике любая сторона противолежит углу 180/7 градусов.
BAC=CAD=ADB=BDC=180/7
AXD=180-CAD-ADB=5*180/7
AXB=180-AXD=2*180/7
ABX=180-BAC-AXB=4*180/7
AX=DX
На отрезке AD выберем точку Y так, что AXY=2*180/7=AXB
Так как в треугольниках ABX и AYX равны все углы и сторона, то они равны. Следовательно AY=AB=a
DXY=AXD-AXY=3*180/7
DYX=180-DXY-XDY=3*180/7
Треугольник XDY равнобедренный. DY=DX=AX=b
AD=AY+DY=a+b
Ответ: a+b
AD=2*b*sin(5*pi/14)
ОтветитьУдалить< - угол. <ABC=pi*5/7. <BAD=pi-<ABC=2*pi/7. Из равенства сторон AB и BC, а так же так как <CAD и <BCA - накрестлежащие, следует, что <CAD=<CAB=<BAC=(2*pi/7)/2=pi/7. Аналогично <ADB=pi/7, тогда <AXD=pi-2*pi/7=5*pi/7.
ОтветитьУдалитьТеперь по теореме косинусов находим AD
AD^2=a^2+a^2-2*a*a*cos(2*pi/7)=4*a^2*(1-cos(2pi/7))/2=
=4a^2*sin^2(pi/7)
Тогда AD=2a*sin(pi/7)
Я только что запостил, почему AD=a+b, не знаю когда старт
ОтветитьУдалитьЕсли задача послана после захвата, большая просьба не публиковать и сообщить условие в личку на назве (чтобы смог перепослать в другую область).
ОтветитьУдалить===Задача
Бильярдист из бильярдных шаров выложил квадрат, а потом из этих же шаров выложил равносторонний треугольник. Количество шаров в стороне квадрата и треугольника отличаются на 2. Сколько у бильярдиста было шаров?
===Решение
Пусть сторона треугольника из Х шаров, тогда сторона квадрата из (Х-2) шаров.
В квадрате (Х-2)^2 шаров.
Чтобы выложить из шаров равносторонний треугольник, необходимо складывать шары 1+2+3+4+...+Х. Количество шаров в треугольнике Х(Х+1)/2
(Х-2)^2=Х(Х+1)/2
Х^2-9Х+8=0
Х=1 Х=8
Нам подходит второй вариант.
Количество шаров (Х-2)^2=(8-2)^2=36
Ответ: 36
Если задача послана после захвата, большая просьба не публиковать и прислать условие в личку на назве.
ОтветитьУдалитьФункциональные равнины (укрепление)
===Задача
У каждого из чисел от 1 до 999999 посчитали суммы цифр. В получившемся ряду опять посчитали суммы цифр. И т.д. пока в ряду не остались только однозначные числа. Получившиеся числа соединили в 999999-значное число и разделили на 9. Чему равен результат?
===Решение
Сумма цифр натурального числа n даёт такой же остаток при делении на 9, как и само число n, поэтому все числа, кратные девяти, превратятся в конце концов в девятки, все числа, дающие остаток 1 при делении на 9 — в единицы, дающие остаток 2 — в двойки, и так далее. Остаётся лишь заметить, что в ряду от 1 до 999999 остатки 1,2,3,4,5,6,7,8,9 дают по 111 111 чисел.
Их сумма равна:
111111*(1+2+3+4+5+6+7+8+9)=111111*45=555555*9
Ответ: 555555
< - угол. <ABC=pi*5/7. <BAD=pi-<ABC=2*pi/7. Из равенства сторон AB и BC, а так же так как <CAD и <BCA - накрестлежащие, следует, что <CAD=<CAB=<BAC=(2*pi/7)/2=pi/7. Аналогично <ADB=pi/7, тогда <AXD=pi-2*pi/7=5*pi/7.
ОтветитьУдалитьТеперь по теореме косинусов находим AD
AD^2=a^2+a^2-2*a*a*cos(5*pi/7)=4*a^2*(1-cos(5pi/7))/2=
=4a^2*sin^2(5pi/14)
Тогда AD=2a*sin(5pi/14)
Видимо, решение E-Science не прошло по техническим причинам (в блоггере иногда почему-то приходится нажимать кнопку "отправить комментарий", затем - ещё раз "отправить комментарий").
ОтветитьУдалитьa+b действительно искомое кратчайшее выражение, область и +15 баллов передаются E-science, с требованием ещё раз отправить обоснование
поправка: я неправильно понял сообщение, на этом ходу область у Назвы, ей +1 балл, сейчас дополнительно выставлю подготовленные укрепления
ОтветитьУдалитьРешение 4, конечно 6 и 8. Треугольное число - 36, это и квадрат 6X6 и равност. тр-ник с 1+2+3+4+5+6+7+8=36 шарами.
ОтветитьУдалитьПовернем чертеж относительно вершины Е (следующей за D, как уже 27 часов назад писал!) на угол пи/7 в семиугольник с вершинами A’=B,C’,D’,E,… Имеем A’B’||AX||G’C’,B’C’||DX. При параллельном проектировании отрезка АХ=b и отрезка A’B’=a вдоль DX на G’C’ получается весь отрезок G’C’, равный AD. Это год висело как анимация на artofproblemsolving, сейчас не видно
ОтветитьУдалить5) Каждое число после такой операции сохраняет остаток от деления на 9 Поэтому в итоге числа преобразуются в остатки от деления на 9, а числа кратные девяти преобразуются в девятку. Если сложит из вместе, то получится число состоящее из 111111 чисел 123456789
ОтветитьУдалить123456789123456789....123456789.
Если его поделить на 9 то получится число
13717421013717421....013717421
тоесть это число состоящее из 111111 чисел 13717421, разделённых нулями
5) квадрат со стороной n шаров и тругольник со стороной m шаров. Тогда всего шаров n^2 или (m+1)m/2.
ОтветитьУдалитьm=n+2
n^2=(n+3)(n+2)/2.
Откуда n=6. А шаров 36
Ответ 36
< - угол. <ABC=pi*5/7. <BAD=pi-<ABC=2*pi/7. Из равенства сторон AB и BC, а так же так как <CAD и <BCA - накрестлежащие, следует, что <CAD=<CAB=<BAC=(2*pi/7)/2=pi/7. Аналогично <ADB=pi/7, тогда <AXD=pi-2*pi/7=5*pi/7.
ОтветитьУдалитьТеперь по теореме косинусов находим AD
AD^2=b^2+b^2-2*b*b*cos(5*pi/7)=4*b^2*(1-cos(5pi/7))/2=
=4b^2*sin^2(5pi/14)
Тогда AD=2b*sin(5pi/14)
3) Ну коль ответ уже известен, то займёмся подгоном.
ОтветитьУдалить<ABC=5pi/7, <BAD=pi-5pi/7=2pi/7. <BAC=<CAD=<BAC=<BAD/2=pi/7, <AXD=pi-<XAD-<XDA=pi-2pi/7=5pi/7, <AXB=pi-<AXD=pi-5pi/7=2pi/7, <ABX=pi-<BAX-<AXB=pi-pi/7-2pi/7=4pi/7. Выразим b через a. Из треугольника ABX
AB/sin(<AXB)=AX/sin(<ABX)
a/sin(2pi/7)=b/sin(4pi/7)
b=a*sin(4pi/7)/sin(2pi/7)=2a*cos(2pi/7)
Теперь Опустим перпендикуляры BH и CK на сторону AD. При этом BH=CK, а HK=BC=AB=a
Найдем AH. Из треугольника AHB имеем, AH=AB*cos(<BAH)=a*cos(2pi/7).
AD=AH+HK+KD=HK+2AH=a+2*a*cos(2pi/7)
Ну и осталось заметить, что последнее слагаемое равно b
AD=a+b
Также через ЛС получено в 23:38
ОтветитьУдалитьФ.равнины,задача 3
Повернем чертеж относительно вершины Е (следующей за D, как уже писал!) на угол пи/7 в семиугольник с вершинами A’=B,C’,D’,E,… Имеем A’B’||AX||G’C’,B’C’||DX. При параллельном проектировании отрезка АХ=b и отрезка A’B’=a вдоль DX на G’C’ получается весь отрезок G’C’, равный AD. Это год висело как анимация на artofproblemsolving, сейчас не видно
Я это 32 часа назад знал, и Вам любой математик скажет. что в кладовых АоПСа это лежит и (прошлой зимой точно) выставлялось.Значит это солиднейшая ссылка ,избавляющая от необходимости повторять давно известное!
Ф.равнины,задача 4
Пусть n число шаров на стороне треугольника,считая вершинные, тогда $\frac {n(n+1)}2=(n-2)^2$
$n^2-9n+8=0$ n=8 Ответ n-2=6
Перефразировано,не помню как в блоге
Те же равнины,Задача 5
При суммировании получаем последовательность 123456789...123456789, где 9-значная последовательность цифр повторяется 111111 раз. При делении на 9 получаем последовательность 137174210137174210...13717421, где 013717421 также повторяется 111111 раз(правда первый 0 незначащий и число 999998-значное)
и ЛС от 21:40
ОтветитьУдалитьФ.равнины,задача 3
Повернем чертеж относительно вершины Е (следующей за D, как уже 27 часов назад писал!) на угол пи/7 в семиугольник с вершинами A’=B,C’,D’,E,… Имеем A’B’||AX||G’C’,B’C’||DX. При параллельном проектировании отрезка АХ=b и отрезка A’B’=a вдоль DX на G’C’ получается весь отрезок G’C’, равный AD. Это год висело как анимация на artofproblemsolving, сейчас не видно
Ф.равнины,задача 4
Решение 4, конечно 6 и 8. Треугольное число - 36, это и квадрат 6X6 и равност. тр-ник с 1+2+3+4+5+6+7+8=36 шарами.
Ответ 36 шаров
Уравнение на n -число шаров в стороне треугольника $(n^2+n)/2=(n-2)^2$
n-2=6,$n^2=36$
ЛС от 21:40
ОтветитьУдалитьЗадача 5 из фун.р.
При суммировании получаем последовательность 123456789...123456789, где 9-значная последовательность цифр повторяется 111111 раз. При делении на 9 получаем последовательность 137174210137174210...13717421, где 013717421 также повторяется 111111 раз(правда первый 0 незначащий)
test
ОтветитьУдалитьИтак, команда E-science первой решила задачи 3 и 4 . Оставшуюся задачу первым взял Zhekas, он и получает контроль над областью
ОтветитьУдалитьИтого E-Science 5+5+3=13 баллов
Zhekas 3+3+5+10=21 балл
назовём прямоугольный параллелепипед хорошим, если его можно разрезать на два равных прямоугольных параллелепипеда. Сколько существует хороших прямоугольных параллелепипедов, имеющих грань 2x6.
ОтветитьУдалитьОтвет 6 штук : 2x6x4; 2x6x1; 2x6x12; 2x6x3; 2x6x2; 2x6x6
Формально говоря,бесконечно много, так как 2х6х 2n разрежется на два по 2х6х n
ОтветитьУдалитьЛюбой прямоугольный параллелепипед можно разрезать на два равных тремя способами параллельно парам граней.
ОтветитьУдалитьНеверно понял условие.
ОтветитьУдалитьУчитывая, что третий размер не ограничен, то таких параллелепипедов существует бесконечное количество, поскольку любой прямоугольный параллелепипед можно разрезать на два равных.
Задача 6.
ОтветитьУдалитьБесконечно много.
E-science получает 5+10=15 баллов и область
ОтветитьУдалитьНазва получает +3 балла
Поправь задачи. 6 - это 7-я, 7 - это 8-я, а 8-ю убери.
ОтветитьУдалить"Чтобы занять область, нужно решить 2 задачи"
ОтветитьУдалитьВ условии 3 задачи и 8-я уже была. Решать две или три???
9-я вернее уже была.
ОтветитьУдалитьОбратите внимание, что задача 9 отличается по формулировке от уже решённой во Фьордах.
ОтветитьУдалитьзадача 9
ОтветитьУдалитьчуть убрав внутрь чётные вершины и выставив наружу нечётные, можно получить 2010-угольник шириной
1/(2*sin(pi/1005))
В таком многоугольнике расстояние от центра до нечётных вершин будет
1/(4*cos(pi/2010)*sin(pi/1005))
а от центра до чётных
(2*cos(pi/2010)-1)/(4*cos(pi/2010)*sin(pi/1005))
(назва)
Задача 7
ОтветитьУдалитьОтвет: стремится к корню из 3
Поскольку
sin(x) = x - (x^3)/6 + O(x^5)
то каждое реккурентное уменьшение числа x равно
(x^3)/6 + O(x^5)
будем называть это "ступенькой", потому что процесс спуска напоминает лесенку, зажатую между графиками x и sin(x)
Количество ступенек на отрезке длиной dx равно
(1+o(1))*6*dx/(x^3)
Поскольку основная часть количества ступенек (бесконечный хвост интеграла) находится около нуля, где часть o(1) становится бесконечно малой, то предел отношения количества ступенек и значения интеграла будет равен 1
Проинтегрируем количество ступенек от x до 1 (или до любой константы a), получим
N ~ (1+o(1))*3/(x^2)
Поэтому в пределе x*sqrt(N) = x*sqrt(3/x^2) = sqrt(3)
(назва)
Задача 8
ОтветитьУдалитьВозьмём очень быстрорастущую последовательность
Напр.,
a_1 = 10
a_k = 10^10^...^10 (a_(k-1) этажей, k>=2)
Теперь положим
c_k = (-1)^k / a_k
Доказательство почти очевидно - добавление следующего члена почти ничего не меняет в области, где у функции уже есть нули, и добавляет ещё один ноль функции при очень больших значениях x
(назва)
"Чтобы занять область, нужно решить ??? задачи"
ОтветитьУдалитьДа, 3, конечно, спасибо, поправил.
ОтветитьУдалитьЗадача 8 Так у функции будет 2009 нулей.
ОтветитьУдалитьЗадача 8
ОтветитьУдалитьВсего одного нуля не хватило? Обидно.
ну тогда там относительно коэффициентов получается линейная система уравнений с матрицей ван-дер-морды, а она невырожденная
поэтому ответ - все коэффициенты - нули
а вообще, правильнее было бы принимать только школьные решения.
(назва)
Назва +10 баллов (за предыдущий ход) +5+10 (за этот ход)
ОтветитьУдалитьИтого +25 баллов и область
Рецензируется решение задачи 9:
ОтветитьУдалитьчуть убрав внутрь чётные вершины и выставив наружу нечётные, можно получить 2010-угольник шириной
1/(2*sin(pi/1005)) НЕВЕРНАЯ ШИРИНА
В таком многоугольнике расстояние от центра до нечётных вершин будет
1/(4*cos(pi/2010)*sin(pi/1005)) НЕВЕРНО
а от центра до чётных
(2*cos(pi/2010)-1)/(4*cos(pi/2010)*sin(pi/1005)) НЕВЕРНО
Таким движением получить 2010-угольник меньшей ширины можно, его точное описание: Берем правильный 1005-угольник шириной 1/2sin(pi/4020), на дугах с центром в каждой вершине, соединяющих две самых удаленных от нее,выбираем посередине еще по точке.
В задаче не было определено построение, но внешнее сходство формул показывает, что имелось в виду.
Подсчет показывает, что расстояние от выбранных точек до ближайших вершин 2*sin(pi/4020)*ширину исходного 2005-угольника, значит они равны 1 и получен 2010-угольник»вписанный в 1005-угольник Рело». Расстояние от центра исходного 1005 –угольника до «четных» вершин 1/[4sin(pi/4020)cos(pi/2010)], до «нечетных» (2cos(pi/2010)-1)/[4sin(pi/4020)cos(pi/2010)]
На олимпиаде за такое решение, не содержащее ни одной верной формулы, можно иногда получить «ПлюсМинус»
Упражнение вдогонку. Построить выпуклый 2010-угольник, со сторонами равными 1, и шириной ЕЩЕ МЕНЬШЕ
ай! 8-ую задачку зачли, но решение - неправильное!
ОтветитьУдалитьматрица вандермонда там и рядом не лежала :(
степени в задаче - произвольные действительные числа, а у вандермонда - последовательные целые
в задаче 9 я разделил pi/2010 пополам и получил pi/1005, ну с кем не бывает :)
а ещё очень хотелось бы посмотреть на школьные решения некоторых уже решённых задач...
(назва)
А при чем тут школьные решения.
ОтветитьУдалитьМожно просто почитать, какие условия:
Задачи должны быть на темы, изучающиеся в средней школе или на 1 курсе не физико-математических вузов. Тематика задач области не обязательно должна совпадать с её названием.
Вот тут ещё один аспект виден:
ОтветитьУдалитьВсё-таки, действительно, решение задачи _перед_ решением о баллах должна увидеть загадывающая команда. Что если организовать это так: каждая команда предоставляет адрес e-mail, на который высылаются решения? При обмене мейлами и решается вопрос удобной вставки рисунка - просто через аттач.