
К карте математического острова
Чтобы занять область, нужно решить 3 задачи:
Задача 11
В однокруговом шахматном турнире (каждый участник играет со всеми по одной партии) участвовали только гроссмейстеры и мастера. После окончания турнира выяснилось, что каждый из участников половину своих очков набрал в партиях против мастеров. Укажите все возможные значения количеств мастеров и гроссмейстеров, участвовавших в турнире. Что можно сказать про общее число участников?
Система начисления очков - традиционная, 1 за победу и 0,5 за ничью.
Задача 12
На шахматной доске 8Х8 достаточно 5 ферзей, чтобы взять под контроль все пустые поля доски. Каково минимальное число ферзей может взять под контроль все пустые поля доски 10Х10?
Задача 13
Каково минимальное число ладей нужно расставить на трехмерной шахматной доске 8Х8Х8 так, чтобы все свободные клетки были под боем? Приведите формулу для количества ладей на доске nXnXn и алгоритм их расстановки.
3-мерная ладья бьёт по трём взаимно перпендикулярным направлениям.
Решённые задачи:
Задача 1. Трёхзначное число нацело разделили на 9, и сумма цифр его уменьшилась на 9. Сколько существует трёхзначных чисел с таким свойством?
Задача 2. Найдите число, десятичная запись которого состоит из чётного количества цифр, и которое увеличится в 6 раз, если его запись разбить на 2 равные части и поменять их местами
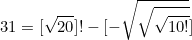
Задача 3: В половину окружности вписан квадрат со стороной a. Найти площадь квадрата, вписанного в окружность того же радиуса.
Задача 4: Чему равна сумма
Задача 5
Составить число 32 из цифр 2,0,1,0 (не меняя порядок), знаков 6 математических действий ,взятия целой части и факториалов, подобно как
Задача 6
Некто ходит по городу из прямоугольных кварталов, ориентированных по сторонам света. Каждый раз, когда он проходит квартал на север, он платит доллар. На юг –получает доллар. На восток- платит столько рублей, сколько у него в кармане долларов. На запад- получает столько рублей, сколько у него в кармане долларов. Обмена валют нет.
Учитывая что в конце прогулки Некто должен вернуться домой, предложите его супруге быстрый способ определить по карте маршрута изменение содержимого его карманов. (Т.е. быстрее, чем просмотр маршрута перекрёсток за перекрёстком и выполнения соответствующих действий. Начальная сумма денег супруге известна)
Задача 7
Дано 10-значное число, все цифры в котором различны.
Число делим на 2, получаем 9-значное частное, теперь делим на 9, получаем 8-значное число. И в 8 и в 9-значном числах все цифры различны. В 8-значном числе нет цифры 9, припишем к нему справа эту цифру. Получим полный квадрат.
Найти исходное 10-значное число.
Задача 8
3-мерный углогрыз, когда ему попадается куб, отгрызает от него угловой кубик (длина стороны съеденного кубика вдвое меньше чем у исходного куба).
Разделите получившееся тело на 8 одинаковых частей.
Задача 9
Докажите, что если число xyz делится на 37 нацело, то и числа yzx и zxy тоже делятся на 37.
P.S. Перебор всех трехзначных чисел, делящихся на 37 как доказательство не принимается.
Задача 10
Найти минимальное n>=4, при котором на плоскости можно расположить n равных эллипсов таким образом, чтобы никакие два эллипса не пересекались и каждый эллипс касался бы трёх других. Доказать возможность или невозможность такого расположения.
Пусть abc - делимое число. xyz - результат (причём x может быть равен нулю).
ОтветитьУдалить(100а+10b+с)/9=100x+10y+z
Если число abc (100а+10b+с) делится на 9 (по условию), то a+b+c также делится на 9 (по признаку делимости). Таких возможных сумм всего три: 9, 18 и 27 (числа выше 27 нельзя разложить на три однозначных слагаемых).
a+b+c=x+y+z+9 (по условию)
a+b+с не может быть равно 9, так как в таком случае x+y+z будет равно нулю.
Если a+b+c=27, тогда abc - это число 999, которое не удовлетворяет условию задачи.
Следовательно a+b+c=18 -> x+y+z=9
Число xyz (100x+10y+z) делится на 9 (по признаку делимости). Следовательно число abc (100а+10b+с) делится на 81. Таких чисел всего 10: 81*n, 2<=n<=12. a+b+c=18 при n=6,7,8,9,11,12 -> x+y+z=9 при n=6,7,8,9,12
Итого, таких чисел существует 5: 81*6=486, 81*7=567, 81*8=648, 81*9=729, 81*12=972
Назва пыталась взять Цифровое Нагорье десантом с воздуха :)
ОтветитьУдалитьНо по условиям маневров, переходить к атаке внутренних областей можно, лишь закрепившись на побережье. Так что присланное решение будет учитываться на следующем ходу, если такие области появятся.
И, в любом случае, в интересах равных шансов, перепошлите, пожалуйста, решение.
ОтветитьУдалитьЗадача 1
ОтветитьУдалитьТаких чисел 5: 486 567 648 729 972
Решение уже присылал.
Задача 2
ОтветитьУдалить6*142857=857142
Nazva получает 5+5+10 = 20 балла
ОтветитьУдалитьОбласть переходит к Nazv'e, которая должна в течение следующего хода укрепить её задачами
Укрепление для цифрового нагорья
ОтветитьУдалить===Условие
В половину окружности вписан квадрат со стороной a. Найти площадь квадрата, вписанного в окружность того же радиуса.
===Решение
Рассмотрим квадрат вписанный в полуокружность.
Радиус окружности, проведённый из вершины квадрата, является гипотенузой треугольника с катетами а и а/2.
R^2=5/4*a^2
Рассмотрим квадрат с искомой стороной х вписанный в окружность.
Его диагональ является гипотенузой треугольника с катетами х.
2х^2=(2R)^2
2x^2=4*5/4*a^2
x^2=5/2*a^2
Укрепление для цифрового нагорья
ОтветитьУдалить===Условие
Вычислить выражение:
http://img403.imageshack.us/img403/5526/35159140.gif
Сумма по n от 1 до 2010 для 5^2011/(25^n+5^2011)
===Решение
Для удобства обозначим функцию суммы как SUM[i,f(i)]
S=SUM[n,5^2011/(25^n+5^2011)] делим на 5^n
S=SUM[n,5^(2011-n)/(5^n+5^(2011-n))]
Положим m=2011-n (диапазон индекса для n=1 m=2010, для n=2010 m=1, т.е. не изменяется)
S=SUM[m,5^m/(5^(2011-m)+5^m)]
Можем менять букву индекса с m на n
S=SUM[n,5^n/(5^(2011-n)+5^n)]
2S=SUM[n,5^(2011-n)/(5^n+5^(2011-n))]+SUM[n,5^n/(5^(2011-n)+5^n)]=SUM[n,(5^(2011-n)+5^n)/(5^(2011-n)+5^n)]=SUM[n,1]=2010
S=1005
R=a/2*5^(1/2) поэтому S=2R^2=2,5 a^2
ОтветитьУдалить(Ian)
Задача 4. Сучча равна 1005, так как симметричные члены дают в парных суммах по 1це
ОтветитьУдалитьIan
4) 1005
ОтветитьУдалить3)S=(5*a^2)/2
ОтветитьУдалитьСкладываем i и 2011-i члены суммы и получаем еденицу. Всего таких едениц получается 1005
ОтветитьУдалитьОтвет 1005
в полуокружности образуем прямоугольный треугольник, вершины которого - это центр окружности нижняя вершина квадрата и соответствующая ей верхняя вершина катета. Гипотенуза равна R, вертикальный катет -a, горизонтальный катет a/2, откуда R=sqrt(a^2+(a/2)^2)=a*sqrt(5)/2
ОтветитьУдалитьдиаметр окружности a*sqrt(5) он же является диагональю квадрата вписанного в данную окружность. тогда катеты
a*sqrt(5/2). Ну и площадь равна a^2*5/2
Здесь возникла сложная ситуация... Дело в том, что я на прошлом ходу совершил 2 ошибки.
ОтветитьУдалить1. Поспешно принял неправильный ответ E-science как правильный и передал команде Мыс Простых чисел. Кроме того, принял ответ Zhekas'a без решения и передал ему Джунгли, хотя уже предупреждал, что ghb взятии укреплений у других команд будет необходимо более развёрнутое обоснование своих действий.
И результатом этих ошибок стало то, что оба участника сошлись за право владения Цифровым Нагорьем.
Выходом из сложившегося положения я считаю следующий:
Решения я не публикую, но после обновления поста о положении на острове на ходе 4
( http://math-zn.blogspot.com/2010/10/4.html )
Они перепосылают свои решения (можно тезисно, т.к. полные решения уже отсылались), и тут решится судьба провинции.
В 4 1005, т. к слагаеиые группируются с краев
ОтветитьУдалитьВ 3й х=1 и х=4, уравнение х2-5х+4=0
А пока Назва получает +1 балл за владение областью
ОтветитьУдалитьЕщё раз повторяю: сигналом о старте штурма будет объявление о завершении обсчёта 4го хода по этой ссылке:
ОтветитьУдалитьhttp://math-zn.blogspot.com/2010/10/4.html
Задача 3(Фальстарт до свистка не считайте)
ОтветитьУдалитьРадиус =а*корень5/2
Сторона=R*корень2
Площадь-2*Rквадрат= 2,5 a2
Задача 4(уже постил)Сумма 1005,так как каждая сумма чисел, равноотстоящих от центра,1
Zhekas получает 3+3=6 баллов
ОтветитьУдалитьE-Science получает 5+5+10=20 баллов и область
Задача 7
ОтветитьУдалить1286375904:2=643187952
643187952:9=71465328
714653280+9=714653289=26733^2
Задача 6
ОтветитьУдалитьПусть дом находится в начале координат. Каждое движение на север отнимает доллар, каждое движение на юг прибавляет доллар. Т.е. изменение количества долларов равна ординате текущего положения Д=Д0-y. По возвращению домой у Некто будет изначальное количество долларов: Д=Д0-0=Д0
Рассмотрим движение вдоль оси абсцисс. При каждом движении количество рублей изменяется так:
На восток (x=x0+1): Р1=Р0-Д=Р0-(Д0-y), Р2=Р0-(Д0-y1)-(Д0-y2)=Р0-2Д0+y1+y2
На запад (x=x0-1): Р1=Р0+Д=Р0+(Д0-y), Р2=Р0+(Д0-y1)+(Д0-y2)=Р0+2Д0-y1-y2
В общем случае: Р=Р0-xД0+К
Поскольку Некто вернётся домой, то: Р=Р0+К
Все движения на восток увеличивают К на значение ординаты, на юг - уменьшают.
ДВ - количество движений на восток вдоль ординаты.
ДЗ - количество движений на запад вдоль ординаты.
К0=0 - все движения по нулевой ординате
К1=1*(ДВ-ДЗ) - движения по ординате 1
Кn=n*(ДВ-ДЗ) - движения по ординате n
К=К0+К1+...+Кn=СУММА[n*(ДВ-ДЗ)]
Р=Р0+К=Р0+СУММА[n*(ДВ-ДЗ)]
ОТВЕТ
Супруге Некто необходимо глядя на маршрут посчитать разницы между количествами восточных и западных движений вдоль каждой ординаты, умножив их на значения ординат и найти сумму полученных произведений. Полученное число и будет приростом рублей. Количество долларов не изменится.
Задача 5
ОтветитьУдалитьhttp://mathurl.com/2uel3al
Задача 6. Попробуйте поискать намного более простую формулу для изменения суммы рублей, она того стоит!
ОтветитьУдалитьНазва получает 5+5=10 баллов
ОтветитьУдалитьE-science получает +1 балл
Так моё решение задачи 6 верное. Почему не засчитана? Потому что не сходится с решением автора?
ОтветитьУдалитьНу, количество долларов не изменится - это очевидно.
ОтветитьУдалитьА чтобы посчитать изменение рублей, нужно из количества ("повороты на запад минус повороты на восток") ЮЖНЕЕ дома вычесть тоже количество СЕВЕРНЕЕ.
Вот-вот.
ОтветитьУдалитьX комментирует...
Задача 6. Попробуйте поискать намного более простую формулу для изменения суммы рублей, она того стоит!
Это ведь обозначает, что задача решена правильно!
Честно говоря, я не пойму, чего требует задача.
ОтветитьУдалитьДля вычисления точного прироста рублей решение, короче, чем моё предыдущее, я не нашёл.
Если требуется всего лишь определить прибавилось или убавилось, тогда обход по часовой стрелке прибавляет рублей, против часовой - отнимает. Этот ответ следует из моего же решения.
Бывают неоднозначные оценки сложная или простая расчетная формула, но здесь слишком явная разница между простым ответом и дающимися. Задача с одной из национальных олимпиад 2003 года, там ответ был дан, и требовалось только его доказать.А у нас же ранг выше, интернет-конкурсы международны:)
ОтветитьУдалитьЭто не международный интернет конкурс, а бенефис e-science. Вы даже не даёте шанса другим участникам.
ОтветитьУдалитьТакого намерения честно не было. Если бы сообщить ответ и попросить - докажите, это в три строчки можно, но в задаче пропадает самое интересное - эврика
ОтветитьУдалитьArmless, такой маршрут (0,0)>(-1,0)>(-1,1)>(0,1)>(1,1)>(1,0)>(1,-1)>(1,-2)>(1,-3)>(1,-4)>(0,-4)>(0,-3)>(0,-2)>(0,-1)>(0,0)
ОтветитьУдалитьПо Вашей формуле +3руб, а в жизни +6руб
Вывод:важно насколько далеко к югу был поворот...
Я пониманию желание загадывающей команды того, чтобы было найдено именно красивое решение задачи (оно действительно красивое). Однако в данном случае считаю более правильным руководствоваться буквой, а не духом правил и передать область Назве.
ОтветитьУдалитьНазва получает 5+10 баллов и область
MagTux, это прежде всего игра и соревнование. Не давать шанса другим участникам - одно из условий достижения победы :) Вы ведь тоже не прочь перекрасить карту в оранжевый цвет?
Решения, полученные по ЛС от E-science:
ОтветитьУдалитьРешение 2-х задач по Цифровому нагорью
=========================================================
=========================================================
Задача 8
3-мерный углогрыз, когда ему попадается куб, отгрызает от него угловой кубик (длина стороны съеденного кубика вдвое меньше чем у исходного куба).
Разделите получившееся тело на 8 одинаковых частей.
=========================================================
Решение.
Исходный куб представим как куб, собранный из 4Х4Х4 =64 маленьких кубиков.
3 центральными сечениями его можно разделить на 8 кубиков 2Х2Х2 - это операция 1.
Операцией 2 назовем изъятие тела из кубика 2Х2Х2 в центральной части исходного куба.
Углогрыз отгрыз у куба угловой куб 2Х2Х2.
В оставшейся части проводим сначала операцию 2, затем 1, получаем 8 равных частей, а именно кубиков 2Х2Х2 с одним отделенным угловым кубиком.
=========================================================
=========================================================
Задача 9
Докажите, что если число xyz делится на 37 нацело, то и числа yzx и zxy тоже делятся на 37.
P.S. Перебор всех трехзначных чисел, делящихся на 37 как доказательство не принимается.
=========================================================
Решение.
Исходное число N1, по условиям N1=100x+10y+z, N1=37k.
При циклической перестановке получаем N2=100y+10z+x.
Заметим, что 111=3*37
Тогда N2=100y+10z+x = 100y+10z+(1000-999)x = 1000x+100y+10z-999x = 10(100x+10y+z)-111*9x = 10N1-37*3*9x=10*37k-37*27x=37(10k-27x)
Получаем, N2 делится на 37.
= = = = = = = = = = = = = = = = = =
Дополнение.
Можно сформулировать такой признак делимости трехзначных чисел на 37: Возьмем наименьшую из цифр числа,сотрем ее но отнимем от каждой из трех остальных.Остальные две будем рассматривать как двузначное число в круговом порядке, начиная с пустого места, например 629...4x7...74. число делится на 37 тогда и только тогда, когда полученное двузначное число делится на 37 (а попросту =0 , 37 или 74)
Из этого признака автоматически следует утверждение задачи, что делимость на 37 не зависит от циклической перестановки цифр.
=========================================================
=========================================================
Последняя задача из Цифрового нагорья
=========================================================
=========================================================
Задача 10
Найти минимальное n>=4, при котором на плоскости можно расположить n равных эллипсов таким образом, чтобы никакие два эллипса не пересекались и каждый эллипс касался бы трёх других. Доказать возможность или невозможность такого расположения.
=========================================================
Решение.
n не может быть нечетным числом, т.к. точек касания должно быть 3n/2.
Четырех быть не может, смотрим извне , на внешней границе их объединения их либо 3 либо 4. Если 3, то большая полуось внутреннего эллипса не поместится в треугольнике с вершинами в точках касания трех остальных.Если 4, то в несамопересекающемся четырехугольнике с вершинами в точках касания существуют две двузвенные ломаные, соединяющие пары противоположных вершин, но не пересекающиеся.
А для n=6 можно построить соответствующий пример
http://radikal.ru/F/s014.radikal.ru/i327/1011/93/acbccd32ad50.png
=========================================================
=========================================================
E-Science получает 15+10=25 баллов и область
ОтветитьУдалитьЗадача 13
ОтветитьУдалитьАлгоритм расстановки ладей для доски 8х8х8 такой:
Разбиваем один уровень доски на 4 квадрата 4х4.
http://img707.imageshack.us/img707/81/chessboard.jpg
На 4-х уровнях в одном из этих квадратов (например, левый верхний) расставляем по 4 ладьи по схеме, чтобы ни одна из них не была под боем:
http://img593.imageshack.us/img593/6518/chessboardl.jpg
На остальных 4-х уровнях в диагональном от выбранного квадрате (правый нижний) расставляем по 4 ладьи аналогично.
Для досок с чётной стороной уровень разбивается на квадраты со стороной n/2
Для досок с нечётной стороной уровень разбивается так, чтобы диагональными были квадраты со сторонами (n+1)/2 и (n-1)/2
Количество ладей соответственно равна сумме площадей двух квадратов.
Количество ладей для "чётных" досок n^2/2
http://mathurl.com/2wlvuwy
Количество ладей для "нечётных" досок ((n+1)/2)^2+((n-1)/2)^2
http://mathurl.com/25sl6qt
Задача 12
ОтветитьУдалить7 ферзей
http://img683.imageshack.us/img683/723/68178794.jpg
К задаче 13 забыл ответ указать
ОтветитьУдалить"Каково минимальное число ладей нужно расставить на трехмерной шахматной доске 8Х8Х8 так, чтобы все свободные клетки были под боем?"
Ответ: 2*(8/2)^2=32
Задача 11
ОтветитьУдалитьПусть было m мастеров и g гроссмейстеров. Всего игроков m + g.
Мастера с мастерами сыграли m(m-1) партий и набрали m(m-1)/2 очков.
Грос-ы с грос-ами сыграли g(g-1) партий и набрали g(g-1)/2 очков.
Мастера с грос-ами набрали m(m-1)/2 очков, а грос-ы с мастерами g(g-1)/2.
Всего партий между мастерами и грос-ами = mg.
m(m-1)/2+g(g-1)/2=mg
(m-g)^2=m+g - общее число участников
Положим m-g=t, тогда m+g=t^2
Суммируем
2m=t^2+t
m=(t^2+t)/2
Вычитаем
2g=t^2-t
g=(t^2-t)/2
Ответ:
m=(t^2+t)/2
g=(t^2-t)/2
t>=2
Общее число участников - полный квадрат натурального числа.
Уточнение к ответу на задачу 11
ОтветитьУдалитьm=(t^2+t)/2
g=(t^2-t)/2
t Є Z, t>=2
Назва получает 5 баллов за решение задачи 11.
ОтветитьУдалитьВ задаче 13 остаётся найти общую формулу.
Поправка: в задаче 13 необходимо доказательство минимальности для N=8
ОтветитьУдалитьЗадачу 11 я поторопился засчитать, она нуждается в уточнении. Пока откат очков не произвожу, предоставляются сутки на доработку.
ОтветитьУдалитьВсё же оброноспособность задачи 11 позволила ей продержаться ещё, как минимум, ход.
ОтветитьУдалить