
Чтобы занять область, нужно решить задачу:
Задача 8
Волк гоняется за зайцем на круглой арене. Максимальные скорости их одинаковы. Сможет ли Волк поймать Зайца?
К карте математического острова
Решенные задачи:
Задача 1. Абориген и Турист сидят на берегу и по очереди берут ракушки из кучи. За один ход можно взять 1, 3 или 7 ракушек, выигрывает тот, кто забирает последнюю. Начинает Абориген, который знает выигрышную стратегию. Каковы шансы у Туриста на победу, если он делает ходы случайным образом, а вначале в куче 2010 ракушек?
Задача 2. В куче лежит N камней. Турист и Абориген поочерёдно берут оттуда по число камней, являющееся степенью четырёх (1, 4, 16, 64 и т.д.). Выигрывает тот, кто забирает последний камень. Начинает Турист. Каждый игрок играет наилучшим для себя образом и не делает ошибок.
Найдите общий вид чисел N, при которых партию выиграет Абориген.
Задача 3
Сколько существует 2010-значных натуральных чисел, которые делятся на 7 при любом порядке своих цифр?
Задача 4
Найти уравнение с целыми коэффициентами, имеющее корень 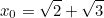
Задача 5
a + b + c = 2010 (a,b,c - целые) Найти остаток от деления a3 + b3 + c3 на 6
Задача 6
Абориген и Турист сидят на берегу и по очереди берут ракушки из кучи. За один ход можно взять 1, n или 7 ракушек, выигрывает тот, кто забирает последнюю. Вначале розыгрыша в куче M ракушек.
Игра заключается в том, что сначала игроки называют числа M, n
Может ли Абориген назвать такое число M, что какое бы n ни назвал Турист, начиная Турист обязательно проиграет.
Задача 7
Утка плавает по круглому озеру со скоростью 2, лиса бегает со скоростью 9 по берегу. Сможет ли оказаться в некоторой точке берега раньше лисы?
В первой задаче не описано условие выигрыша.
ОтветитьУдалитьСпасибо, поправил
ОтветитьУдалитьЗадача 1.
ОтветитьУдалитьШансы 100%. После каждого хода четность ракушек меняется. Соответственно, будет сделано четное число ходов, т.е. последний ход сделает Турист.
Ответ: 100%
Задача 2.
N=5k+1+-1 (N=5k или N=5k+2), где k - целое число >= 0.
Зарегистрировался, напишу свой вариант еще раз.
ОтветитьУдалитьЗадача 1.
Вероятность 100%. Четность ракушек в куче меняется после каждого хода. Значит, будет сделано четное число ходов. Значит, Турист выиграет вне зависимости от его ходов.
Ответ. Вероятность 100%.
Задача 2.
Ответ. N=5k+1±1
Задача 1 решена, для задачи 2 требуется более полное обоснование
ОтветитьУдалитьNazva получает 5 баллов
Решение задачи 2:
ОтветитьУдалитьСоставим таблицы побед/поражений для первых 5 чисел (относительно того, чей сейчас ход):
0 - поражение (так как предыдущий ход принес победу сопернику)
1 - победа (так как мы можем своим ходом забрать последний камень)
2 - поражение (так как своим единственным ходом мы сводим игру к выигрышной ситуации для соперника)
3 - победа (так как своим ходом мы можем свести игру к проигрышной для соперника ситуации)
4 - победа (так как своим ходом мы можем забрать 4 оставшихся камня)
Все степени 4 оканчиваются либо на 4, либо на 6. Значит, они все принадлежат к числам вида
5k±1. Какое бы ни было числа камней в куче первоначально, соперник своим вторым ходом может вернуть кол-во к такому же виду (если было 5k+n, то можно сделать 5m+n) (если Вы уберете 5k+1 камней, то соперник уберет 5m-1, и наоборот). То есть числа вида 5k+2 и 5k являются проигрышными для начинающего игру, так как соперник сможет к одному из ваших ходов оставить либо 2 камня, либо 0 камней.
Теперь докажем, что остальные числа являются выигрышными. Из чисел вида 5k+1 или 5k+3 мы можем перейти к проигрышной ситуации для соперника, убрав из кучи один камень. Из чисел вида 5k+4 мы можем перейти к проигрышной ситуации для соперника, убрав из кучи 4 камня.
Назва получает 10+5=15 баллов и область
ОтветитьУдалить===Условие
ОтветитьУдалитьa + b + c = 2010 (a,b,c - целые)
Найти остаток от деления a3 + b3 + c3 на 6
===Решение
Рассмотрим выражение a^3 + b^3 + c^3 - (a + b + c).
a^3 + b^3 + c^3 - (a + b + c) = a(a^2 - 1) + b(b^2 - 1) + c(c^2 - 1) = a(a - 1)(a + 1) + b(b - 1)(b + 1) + c(c - 1)(c + 1).
x(x - 1)(x + 1) делится как и на 2 (ввиду того, что произведение двух последовательных чисел делится на 2), так и на 3 (ввиду того, что произведение трех последовательных чисел делится на 3), а потому и на 6.
Значит правая часть преобразований делится на 6. По условию a + b + c = 2010 делится на 6, потому и a^3 + b^3 + c^3 делится на 6.
Ответ: 0
===Условие
ОтветитьУдалитьНайти уравнение с целыми коэффициентами, имеющее корень x0 = √2 + √3.
===Решение
Пусть x0, x1 - корни уравнения (x - x0)(x - x1) = 0, где x0 = √2 + √3. Преобразовывая уравнение получим:
x^2 - (x0 + x1) + x0x1 = 0. Сделаем один из коэффициентов целым, положив x1 = - √2 - √3. Уравнение примет вид:
x^2 - (√2 + √3)^2 = 0.
x^2 - (5 + 2√6) = 0.
x^2 - 5 = 2√6. Подносим в квадрат.
x^4 - 10x^2 + 25 = 24.
x^4 - 10x^2 + 1 = 0.
Подставив √2 + √3, можно убедиться, что данное число является корнем указанного уравнения с целыми коэффициентами.
===Условие
ОтветитьУдалитьСколько существует 2010-значных натуральных чисел, которые делятся на 7 при любом порядке своих цифр?
===Решение
Такие числа состоят только из семёрок и нулей. Ответ: 2^2009
Задача 5
ОтветитьУдалитьa + b + c = 2010 (a,b,c - целые) Найти остаток от деления a^3 + b^3 + c^3 на 6
Решение.
Т.к. a + b + c = 2010 (a,b,c - целые), то из 3-х чисел или 1 или 3 - четные, тогда abc четное, т.е. abc=2m
a^3 + b^3 + c^3 = (a+b+c)(a^2+b^2+c^2-ab-ac-bc) + 3abc = 2010 (a^2+b^2+c^2-ab-ac-bc) + 3*2m = 6 (335(a^2+b^2+c^2-ab-ac-bc) + m)
т.е. остаток от деления a^3 + b^3 + c^3 на 6 - 0.
Это число должно состоять только из семёрок и из нулей.
ОтветитьУдалитьТаких чисел(2010- значных) 2^2009. В старшем разряде стоит 7, а в остальных 2009 либо 7 либо 0.
2^2009
4)
ОтветитьУдалитьx=sqrt(2)+sqrt(3) Возведём в квадрат
x^2=2+2sqrt(6)+3
x^2-5=2sqrt(6) возведём в квадрат
(x^2-5)^2=4*6
(x^2-5)^2-24=0
x^4-10x^2+25-24=0
x^4-10x^2+1=0
остатки от деления на 6 при возведении числа в куб не меняются.
ОтветитьУдалитьa^3+b^3+c^3 mod 6=a+b+c mod 6 = 2010 mod 6=0
4)
ОтветитьУдалить(x^2-5)^2=72
(Назва)
ой!
ОтветитьУдалитьназва не может захватить свою область, решив свои же задачки :)
удалите плз
решения приходили от E-science через ЛС на форуме в 20:30
ОтветитьУдалитьЗадача 4
х4-10х2+1=0
х2=5+-2корень6
но квадрат данного в условии числа как раз 5+2корень6
Задача 5
a + b + c = 2010 (a,b,c - целые) Найти остаток от деления a^3 + b^3 + c^3 на 6
Решение.
Т.к. a + b + c = 2010 (a,b,c - целые), то из 3-х чисел или 1 или 3 - четные, тогда abc четное, т.е. abc=2m
a^3 + b^3 + c^3 = (a+b+c)(a^2+b^2+c^2-ab-ac-bc) + 3abc = 2010 (a^2+b^2+c^2-ab-ac-bc) + 3*2m = 6 (335(a^2+b^2+c^2-ab-ac-bc) + m)
т.е. остаток от деления a^3 + b^3 + c^3 на 6 - 0.
и в 23:38:
ОтветитьУдалитьЗадача 3
Что будет при перемене местами двух соседних?(а последовательностью таких перемен можно получить любой порядок цифр)Число изменится на $10^k(10a+b-10b-a)=9*10^k(a-$,то есть существовавшая предположительно делимость на 7 не изменится только если цифры сравнимы по модулю 7
По признаку делимости на 7 нужная сумма $\sum_n(a_{6n+1}+3a_{6n+2}+2a_{6n+3}+6a_{6n+4}+4a_{6n+5}+5a_{6n+6})$ делиться на 7 будет,т.к. содержит 335 полных слагаемых.Значит, исходное число и все его перестановки будут делиться на 7 тогда и только тогда,когда все цифры равны по модулю 7.Если это значение по модулю 7 =3,4,5,6-по одному числу. Если=1 или 2,то по $2^{2010}$ чисел.
Если =0.Из чисел 0 и 7 можно составить $2^{2010}$ чисел , считая 0 и число из одних 7-к.Отбросим не 2010-значные, в число которых включаем и "нульзначное"000..0.Их $2^{2009}$Получаем ответ
$N=4+3*2^{2010}-2^{2009}=4+5*2^{2009}$
Zhekas получает 3+3=6 баллов
ОтветитьУдалитьE-Science получает 5+5+5+10=25 баллов и область
Задача 7
ОтветитьУдалитьПусть скорость утки 2v, лисы - 9v, R - радиус озера.
Длина пути лисы по берегу = 2piR
Утка от центра озера может двигаться так (по спирали), чтобы лиса была на одном диаметре с уткой. Таким образом она может доплыть до окружности длиной 2piR*2/9 радиусом R*2/9
Путь до берега x=R-R*2/9=R*7/9
Время преодолевания (R*7/9)/2v=7R/18v
Путь лисы равен половине окружности озера piR
Время преодолевания piR/9v=2piR/18v ~ 6,28R/18v
Т.е лиса добежит быстрее.
Этот комментарий был удален автором.
ОтветитьУдалитьЗадача 8
ОтветитьУдалитьПоскольку в условии не оговорено, то считаем реакцию волка мгновенной.
Если заяц будет бежать по прямой от волка, то расстояние между ними будет постоянным. Если заяц сменит направление, то расстояние сократится.
Доказать это просто.
Пусть в определённый момент времени заяц сменил направление. Тогда через как угодно малый отрезок времени точка положения волка, точка положения зайца и прежняя точка положения зайца до реакции волка образует треугольник. Изначальное расстояние между волком и зайцем равна сумме двух сторон треугольника (от волка до точки поворота и от точки поворота до зайца). Поскольку волк побежит по третей стороне треугольника, то по свойству треугольника расстояние сократится.
В итоге волк догонит зайца.
Задача 7 (так хочется наконец захватить что-нибудь, что поневоле делаю ошибки)
ОтветитьУдалитьПоскольку скорости точно определены, то предыдущее решение в общем виде можно уточнить. Т.е. выбросить буквы V. При этом ответ остаётся тем же.
Задача 6.
ОтветитьУдалитьДа, может.
Чтобы это доказать, нужно найти формулы для М, при которых начинающий проигрывает.
При нечетных n (n=3, n=5), начинающий проигрывает, если М - четное число.
При n=2, начинающий проигрывает, если М=3k, где k - любое натуральное число.
При n=4, начинающий проигрывает, если M=8p , M=8p+2 , M=8p+5 (возможен любой вариант), где р - любое натуральное число.
При n=6, начинающий проигрывает, если M=12q , M=12q+2 , M=12q+4 (возможен любой вариант), где q - любое натуральное число.
Получаем, что начинающий проигрывает при М=24р вне зависимости от n. Например, можно взять М=24.
Ответ. Да, это возможно.
Задача 6, Um-nik РЕШЕНА
ОтветитьУдалитьЗадача 7 НЕВЕРНО
Задача 8 НЕВЕРНО
Назва получает 5 баллов
ОтветитьУдалитьE-science получает 1 балл
7) сможет
ОтветитьУдалитьнапример, пусть утка плавает по "утиному" кругу радиуса 2/9, находясь в противофазе от лисы (центр пруда лежит на отрезке лиса-утка), теперь утке достаточно начать плыть по касательной к "утиному" кругу, и она опередит лису. У касательной два направления, нужно только выбрать правильное :)
(назва)
8) сможет
ОтветитьУдалитьтактика догоняющего - держаться на одном радиусе с убегающим
если убегающий бежит по кругу, то за четверть круга его догонят
http://img808.imageshack.us/img808/7664/83819916.png
если убегающий бежит не по кругу, то это только ускорит радиальное сближение
(назва)
Взата одна задача, Назва +5 баллов
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьПоследний комментарий был для джунглей.
ОтветитьУдалитьЗадача №8.
ОтветитьУдалитьВолк не сможет догнать Зайца.
Лиса и волк гонятся за зайцем по числовому лучу. Сейчас между ними расстояние 7 делений. Успеет ли заяц спрятаться в своем домике , если его прыжок - 1 деление , прыжок лисы - 2 деления , прыжок волка - 3 деления.
ОтветитьУдалить