Чтобы занять область, нужно решить 3 задачи:
Задача 7
Даны шесть одинаковых по размеру кубиков разного веса: 1, 2, 3, 4, 5 и 6 грамм. Hа кубиках написаны числа от 1 до 6. Требуется с помощью чашечных весов (без гирь) доказать или опровергнуть утверждение: "Числа на кубиках соответствуют их весу в граммах". За какое минимальное количество взвешиваний это можно сделать (и как)?
Весы не отрегулированы, взвешивать на равенство весов нельзя, но разницу в весе в хотя бы в 1 грамм покажут верно.
Задача 8
Найти последние 3 цифры числа
(в последнем множителе 2010 троек)
Задача 9
Дана функция f(x)=x2+6x+6
решить уравнение:
f(f(f( ... f(x) ... )))=0
Взятие функции происходит 2010 раз.
К карте математического острова
Решенные задачи:
Задача 1. Для скольких натуральных чисел n от 1 до 1000 включительно число 2nn является кубом натурального числа?
Задача 2. В сейфе хранится несколько колье. В каждом из них одинаковое количество бриллиантов (больше одного). Если бы было известно общее количество бриллиантов в сейфе, то можно было бы однозначно определить, сколько в нём колье. Сможете ли вы узнать это, если мы вам скажем, что бриллиантов в сейфе от 200 до 300?
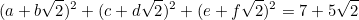
Задача 3
Сколько существует наборов из 6 рациональных чисел a,b,c,d,e,f таких, что
Задача 4
Продолжить последовательность чисел 1, 21, 31, 34, 41, 43, ...
//По традиции оценивания задач на последовательности, засчитываются и не совпадающие с загаданным правила, если те не используют для своего вывода всех известных членов (аппроксимация многочленом 5-й степени - не решение).
Задача 5
В начале дана дробь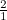 
. Умножим числитель и знаменатель на удвоенный числитель и вычтем из нового числителя единицу, будем повторять эту операцию многократно. К какому числу будет стремиться дробь?
Задача 6
В треугольнике АВС угол В - прямой. На гипотенузе АС отметили точку О. Через точку О провели прямую КО, где КО||ВС, К лежит на АВ. Через точку О провели также прямую МО, где МО||АВ, М лежит на ВС. Где должна быть отмечена точка О, чтобы длина отрезка КМ была наименьшей?
Задача 1
ОтветитьУдалить2n^n будет кубом числа при n кратное 3, а также единственное исключение n=2.
Итого 1000 div 3 + 1=334
Ответ 334
И обе крепости сохраняют обороноспособность!
ОтветитьУдалить2n^n может быть кубом числа только при n=2^x
ОтветитьУдалитьНепосредственным перебором х от 0 до 9 получаем: n=2, n=4, n=128, n=256
Ответ: 4
Um-nik Nazva.net
Задача 1
ОтветитьУдалитьОтвет: n=2, 4, 128, 256
Вычислил так: если 2n^n - куб, то 2n^n/n^3 - тоже куб.
Следовательно если число 2n^(n mod 3) - куб, то и число 2n^n также куб.
А дальше подбор.
2) 17 штук
ОтветитьУдалить1) Я насчитал 4 числа
ОтветитьУдалитьn=2, 128, 256, 686
1) Всё же 5
ОтветитьУдалить2, 4, 128, 256, 686
1) и всё же 4.
ОтветитьУдалитьn=4 -не подходит
Задача 1.
ОтветитьУдалить2n^n будет кубом числа только в случае n=2^x, где х - натуральное число. Так как n<=1000, x<=9. Перебором х удостоверяемся, что для n подходят значения 2, 4, 128 и 256.
Ответ. Для 4 чисел.
Задача 2.
Это число должно иметь всего 1 делитель (кроме себя и единицы). То есть, это должен быть квадрат простого числа. Единственное подходящее число - 17^2=289.
Ответ. В сейфе 17 колье.
Задача 2 решена!
ОтветитьУдалитьЗадача 1 держится!
Здесь произошла интересная ситуация: первым на задачу 2 ответил zhekas, однако, не имеющий общей границы с этой областью.
Я решил проявить волюнтаризм и дать обоим решившим по 5 баллов.
Nazva получает 5 баллов
Zhekas получает 5 баллов
Для занятий области осталось решить одну задачу!
Задача 1.
ОтветитьУдалитьЕсли имеется в виду (2n)^n, то ответ - 336.
Если 2(n^n), то ответ - 4.
Если n делится на 3, то n^n куб, значит 2*n^n кубом быть не может. То есть n не должно быть кратно 3. Если непарный p простой делитель n, то он должен входить в разложение n на простые множители в степени кратной 3, потому что n на 3 не делится, а в числе 2*n^n он в степени кратной 3. Поскольку 5^6 больше 1000, то непарное простое число может входить в разложение n на простые числа только в третьей степени.
ОтветитьУдалитьРассмотрим 2 случая:
1) n имеет непарный простой делитель. Поскольку n должно быть парным, то возможны только такие варианты 2*125, 4*125, 2*343. Легко увидеть, что нам подходит только 2*125.
2) n - степень двойки. Перебором можно убедится, что подходят 2, 4, 128 и 256.
Ответ: 5 чисел.
для 1-вой задачи, вроде ответы у всех верны.
ОтветитьУдалитьтогда предложу такое решение:
2n^n будет кубом числа только в случае n=2^x, где х - натуральное число, x<=9
2*n^n = 2*(2^x)^n = 2*2^(x*n) = 2^(x*n + 1), следовательно
(x*n + 1) mod 3 = 0
Ответ: n=2, 4, 128, 256
Nikenbiraki (Nazva.net)
Да, на всякий случай: В задаче 2 порядок действий стандартный: сначала n возводится в степень n, и затем результат умножается на 2.
ОтветитьУдалитьНу что можно сказать... Буквально чудом крепость выдержала штурм на этом ходу. Единственный невзятый бастион помог ей устоять
ОтветитьУдалитьЕсли n делится на 3, то n^n куб, значит 2*n^n кубом быть не может. То есть n не должно быть кратно 3. Если непарный p простой делитель n, то он должен входить в разложение n на простые множители в степени кратной 3, потому что n на 3 не делится, а в числе 2*n^n он в степени кратной 3. Поскольку 5^6 больше 1000, то непарное простое число может входить в разложение n на простые числа только в третьей степени.
ОтветитьУдалитьРассмотрим 2 случая:
1) n имеет непарный простой делитель. Поскольку n должно быть парным, то возможны только такие варианты 2*125, 4*125, 2*343. Проверкой удостоверяемся, что нам подходят только 2*125 и 2*343.
2) n - степень двойки. Перебором можно убедится, что подходят 2, 4, 128 и 256.
Ответ: 6 чисел.
5 штук 2,4,128,256,686 (E-science/)
ОтветитьУдалить1) 2,2^2,2^6,2^7,2*7^3
ОтветитьУдалить5 чисел
(Назва)
Ой, ошибся
ОтветитьУдалить1) 2,2^2,2^7,2^8,2*7^3
5 чисел
(Назва)
Задача 1
ОтветитьУдалитьЧисло S=2n^n является кубом в двух случаях:
1) S=2*(2*m^3)^n=2^(n+1)*m^3n
n+1 mod 3 = 0 -> n mod 3 = 2
2*m^3<=1000 -> m<=7
Подходящие значения n: 2, 128, 686
2) S=2*(4*m^3)^n=2^(2n+1)*m^3n
2n+1 mod 3 = 0 -> n mod 3 = 1
4*m^3<=1000 -> m<=6
Подходящие значения n: 4, 256
Ответ: 5 чисел : 2,4,128,256,686
E-Science получает 10+5=15 баллов и область
ОтветитьУдалитьНазва получает +3 балла
4)
ОтветитьУдалитьЧисло 6k-5 записано в (k+1)-чной системе счисления
(назва)
ой!
ОтветитьУдалитьназва не граничит с этой областью и не может её захватить...
удалите плз
Граничащие с областью игроки не атаковали, E-science +1 балл за сохранение территории
ОтветитьУдалитьE-science +1 балл за сохранение территории
ОтветитьУдалитьПро двое суток я понял. А когда можно начинать атаковывать?
ОтветитьУдалитьМожно атаковать в начале первого полухода (т.е. первых суток).
ОтветитьУдалитьE-science получает +1 балл за сохранение области
ОтветитьУдалить5)
ОтветитьУдалитьк корню из 3
Заметим, что если дробь такова, что для некоторого числа х её числитель равен
А(х) = (х+1/х)/2,
и знаменатель равен
В(х) = (х-1/х)/(2*корень(3)),
то после преобразования дробь
А(х) / В(х)
превратится в дробь
А(х*х) / В(х*х)
Это проверяется подстановкой в формулы из условия.
Исходная дробь соответствовала
х = 2 + корень(3)
поэтому в пределе получим отношение
А(Х) / В(Х)
где Х стремится к бесконечности.
Это отношение равно корню из 3
(назва)
Крепость устояла
ОтветитьУдалитьХребет натуральных чисел, задача 5
ОтветитьУдалитьНу что там непонятно в предыдущем решении?
Рассмотрим две функции A(x) и B(x), которые я там выписал, и выполним три шага:
1) Заметим, что если переменная x равна 2+sqrt(3), то A(x)=2 совпадает с числителем первоначальной дроби, а B(x)=1 - с её знаменателем
2) Ещё заметим, что если в числителе дроби стоит A(x), а в знаменателе - B(x), то после применении операции над дробью в числителе будет A(x^2), а в знаменателе B(x^2). Да, вот такая хитрая пара функций, специально подбирал. :) С помощью этих функций можно явно выписать формулу для любой дроби из получающейся последовательности.
3) После многократного применения этой операции дробь будет стремиться к пределу A(x)/B(x) при x -> inf
Этот предел легко вычисляется и равен sqrt(3)
(назва)
Задача 4
ОтветитьУдалитьВзяты числа 1,7,13,... из арифметической прогрессии с разностью 6
и записаны в системах счисления 2,3,4,... соответственно
(назва)
Задача 3
Если бы было хоть одно решение, то изменив знаки чисел b,d,f, мы получили бы решение уравнения, точно такого же, но в правой части которого стоит число 7-5*sqrt(2), а оно отрицательное.
Значит, решений нет.
Назва получает 15+10=25 баллов и область
ОтветитьУдалитьE-Science получает 5+10=15 баллов и область
ОтветитьУдалитьЗадача №9
ОтветитьУдалить$x=-3\pm(3)^{(1/2)^{2010}}$
Задача №8
ОтветитьУдалить059